题目内容
18．
如图，AB=AE，BC=ED，AF⊥CD，∠B=∠E．F是CD的中点吗？为什么？
分析 连接AC，AD，可证△ABC≌△AED，可得AC=AD，由AF⊥CD，根据等腰三角形的性质三线合一证得F是CD的中点．
解答 
解：是，
如图，连接AC、AD，
在△ABC与△AED中，
$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠F}\\{BC=DE}\end{array}\right.$，
∴△ABC≌△AED，
∴AC=AD，
∵AF⊥CD，
∴CF=DF，
∴F是CD的中点
点评 本题考查了全等三角形的判定，考查了全等三角形对应角、对应边相等的性质，本题中辅助线的作法是解题的关键．
练习册系列答案
相关题目
9．为了加强公民的节水意识，合理利用水资源，某市采用价格调控手段达到节水的目的，该市自来水收费价格见表，例如：某户居民1月份用水15立方米，则应收水费：2×10+3×（15-10）=35（元）．
（1）若该户居民2月份用水24立方米，则应收水费多少元？
（2）若该户居民3、4月份共用水26立方米（3月份用水量不超过10立方米），共交水费60元，则该户居民3、4月份各用水多少立方米？
| 每月用水量 | 单价 |
| 不超出10立方米的部分 | 2元/立方米 |
| 超出10立方米不超出20立方米部分 | 3元/立方米 |
| 超出20立方米的部分 | 4元/立方米 |
（2）若该户居民3、4月份共用水26立方米（3月份用水量不超过10立方米），共交水费60元，则该户居民3、4月份各用水多少立方米？
如图，在△ABC中，AD平分∠BAC，AB+BD=AC，试讨论：∠B与∠C有什么样的等量关系？
13．
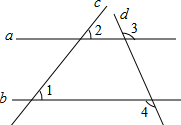如图，若∠1=40°，∠2=40°，∠3=110°36′，则∠4的度数为（ ）
如图，若∠1=40°，∠2=40°，∠3=110°36′，则∠4的度数为（ ）| A． | 68.6° | B． | 110°36′ | C． | 68.4° | D． | 69.4° |
如图，四边形ABDE，ACFG都是正方形．求证：
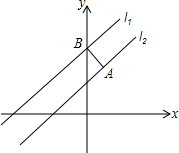如图所示，已知两条直线l1：y=2x+7，l2：y=2x+5，在l2上任取一点A，过点A作直线l1的垂线，垂足为B点，求AB的长．