题目内容
17.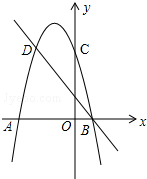 如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.(1)求二次函数的解析式;
(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围;
(3)若直线与y轴的交点为E,连结AD、AE,求△ADE的面积.
分析 (1)直接将已知点代入函数解析式求出即可;
(2)利用函数图象结合交点坐标得出使一次函数值大于二次函数值的x的取值范围;
(3)分别得出EO,AB的长,进而得出面积.
解答 解:(1)设二次函数的解析式为y=ax2+bx+c(a≠0,a、b、c常数),
根据题意得 $\left\{\begin{array}{l}{9a-3b+c=0}\\{a+b+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$,
所以二次函数的解析式为:y=-x2-2x+3;
(2)如图,一次函数值大于二次函数值的x的取值范围是:x<-2或x>1.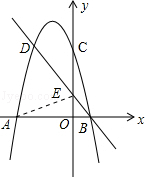
(3)∵对称轴:x=-1.∴D(-2,3);
设直线BD:y=mx+n 代入B(1,0),D(-2,3):
$\left\{\begin{array}{l}{m+n=0}\\{-2m+n=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-1}\\{n=1}\end{array}\right.$,
故直线BD的解析式为:y=-x+1,
把x=0代入求得E(0,1)
∴OE=1,
又∵AB=4
∴S△ADE=$\frac{1}{2}$×4×3-$\frac{1}{2}$×4×1=4.
点评 此题主要考查了待定系数法求一次函数和二次函数解析式,利用数形结合得出是解题关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
5.在平面直角坐标系xOy中,第一象限内的点P在反比例函数的图象上,如果点P的纵坐标是3,OP=5,那么该函数的表达式为( )
| A. | y=$\frac{12}{x}$ | B. | y=-$\frac{12}{x}$ | C. | y=$\frac{15}{x}$ | D. | y=-$\frac{15}{x}$ |
12.若直线y=ax+b(a≠0)在第二、四象限都无图象,则抛物线y=ax2+bx+c( )
| A. | 开口向上,对称轴是y轴 | B. | 开口向下,对称轴平行于y轴 | ||
| C. | 开口向上,对称轴平行于y轴 | D. | 开口向下,对称轴是y轴 |
2.一个不透明的口袋里有4张形状完全相同的卡片,分别写有数字1,2,3,4,口袋外有两张卡片,分别写有数字2,3,现随机从口袋里取出一张卡片,则两次摸出的卡片的数字之和等于4的概率( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
9.如果点A(-4,y1),B(-1,y2),C(3,y3)都在反比例函数$y=\frac{k}{x}(k<0)$的图象上,那么y1,y2,y3的大小关系是( )
| A. | y1<y3<y2 | B. | y3<y1<y2 | C. | y1<y2<y3 | D. | y3<y2<y1 |
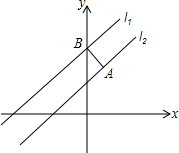 如图所示,已知两条直线l1:y=2x+7,l2:y=2x+5,在l2上任取一点A,过点A作直线l1的垂线,垂足为B点,求AB的长.
如图所示,已知两条直线l1:y=2x+7,l2:y=2x+5,在l2上任取一点A,过点A作直线l1的垂线,垂足为B点,求AB的长.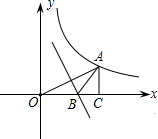 如图,点A(3,m)在双曲线$y=\frac{3}{x}$上,过点A作AC⊥x轴于点C,线段OA的垂直平分线交OC于点B,则△ABC的周长的值为( )
如图,点A(3,m)在双曲线$y=\frac{3}{x}$上,过点A作AC⊥x轴于点C,线段OA的垂直平分线交OC于点B,则△ABC的周长的值为( ) 如图,二次函数y=x(x-2)(0≤x≤2)的图象,记为C1,它与x轴交于O、A1两点;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C2016.若P(4031,m)在第2016段图象C2016上,则m=1.
如图,二次函数y=x(x-2)(0≤x≤2)的图象,记为C1,它与x轴交于O、A1两点;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C2016.若P(4031,m)在第2016段图象C2016上,则m=1.