题目内容
10.若x=$\frac{\sqrt{2}-1}{\sqrt{2}+1}$,y=$\frac{\sqrt{2}+1}{\sqrt{2}-1}$,则xy=1,x+y=6,x-y=-4$\sqrt{2}$,x2+y2=34.分析 首先化简x,y,再分别代入即可.
解答 解:∵x=$\frac{\sqrt{2}-1}{\sqrt{2}+1}$=3-2$\sqrt{2}$,y=$\frac{\sqrt{2}+1}{\sqrt{2}-1}$=3$+2\sqrt{2}$,
∴xy=(3$-2\sqrt{2}$)(3$+2\sqrt{2}$)=9-8=1;
x+y=3$-2\sqrt{2}$$+3+2\sqrt{2}$=6;
x-y=3-2$\sqrt{2}$-(3$+2\sqrt{2}$)=-4$\sqrt{2}$;
x2+y2=(x+y)2-2xy=62-2×1=34,
故答案为:1,6,-4$\sqrt{2}$,34.
点评 本题主要考查了二次根式的化简求值,先化简再代入是解答此题的关键.

练习册系列答案
相关题目
18.对于二次函数y=3(x-1)2,下列结论正确的是( )
| A. | 当x取任何实数时,y的值总是正的 | B. | 其图象的顶点坐标为(0,1) | ||
| C. | 当x>1时,y随x的增大而增大 | D. | 其图象关于x轴对称 |
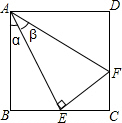 如图,E是正方形ABCD中BC边上的任意一点,连接AE,过点E作EF⊥AE交CD于点F,设∠BAE=α,∠EAF=β.求证:若E是BC的中点,则α=β,AF=AB+CF.
如图,E是正方形ABCD中BC边上的任意一点,连接AE,过点E作EF⊥AE交CD于点F,设∠BAE=α,∠EAF=β.求证:若E是BC的中点,则α=β,AF=AB+CF.