题目内容
20.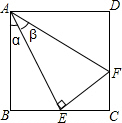 如图,E是正方形ABCD中BC边上的任意一点,连接AE,过点E作EF⊥AE交CD于点F,设∠BAE=α,∠EAF=β.求证:若E是BC的中点,则α=β,AF=AB+CF.
如图,E是正方形ABCD中BC边上的任意一点,连接AE,过点E作EF⊥AE交CD于点F,设∠BAE=α,∠EAF=β.求证:若E是BC的中点,则α=β,AF=AB+CF.
分析 根据同角的余角相等可得∠AEb=∠EFC,∠BAE=∠FEC,然后求出△ABE和△ECF相似,根据相似三角形对应边成比例可得$\frac{AE}{BE}=\frac{EF}{CF}$,然后根据两组边对边对应成比例且夹角相等,证明△AEF∽△ECF,再根据相似三角形对应角相等可得∠FAE=∠FEC,过点E作EH⊥AF于H,根据角平分线上的点到角的两边距离相等可得BE=HE,利用“HL”证明△ABE和△AHE,根据全等三角形对应边相等可得AB=AH,同理可得FC=FH,然后求出AF=AB+CF.
解答 解:∵EF⊥AE,
∴∠AEB+∠FEC=90°,
∵∠FEC+∠EFC=90°,
∴∠AEB=∠EFC,
∴∠BAE=∠FEC,
又∵∠B=∠C=90°,
∴△ABE∽△ECF,
∴$\frac{AE}{BE}=\frac{EF}{CF}$,
∵点E是BC的中点,
∴BE=CE,
∴$\frac{AE}{CE}=\frac{EF}{CF}$,
又∵∠AEF=∠C=90°,
∴△AEF∽△ECF,
∴∠FAE=∠FEC,
∴∠BAE=∠FAE,
即α=β.
如图,
过点E作EH⊥AF于H,
则BE=HE,
在Rt△ABE和Rt△AHE中,
$\left\{\begin{array}{l}{AE=AE}\\{BE=HE}\end{array}\right.$,
∴Rt△ABE≌Rt△AHE(HL),
∴AB=AH,
同理可得△ECF≌△EHF,
∴FC=FH,
∵AF=AH+FH
∴AF=AB+CF.
点评 本题考查了矩形的性质,全等三角形的判定与性质,相似三角形的判定与性质,解直角三角形,熟记各性质是解题的关键.

练习册系列答案
相关题目
11. 如图,菱形ABCD的两条对角线相交于O,若菱形的面积为24,AC=8,则菱形的周长为( )
如图,菱形ABCD的两条对角线相交于O,若菱形的面积为24,AC=8,则菱形的周长为( )
 如图,菱形ABCD的两条对角线相交于O,若菱形的面积为24,AC=8,则菱形的周长为( )
如图,菱形ABCD的两条对角线相交于O,若菱形的面积为24,AC=8,则菱形的周长为( )| A. | 20 | B. | 15 | C. | 10 | D. | 24 |
5.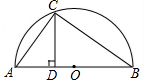 如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过点C作CD⊥AB交AB于点D.若cos∠BCD=$\frac{3}{5}$,AC=4,则BC的长为( )
如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过点C作CD⊥AB交AB于点D.若cos∠BCD=$\frac{3}{5}$,AC=4,则BC的长为( )
 如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过点C作CD⊥AB交AB于点D.若cos∠BCD=$\frac{3}{5}$,AC=4,则BC的长为( )
如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过点C作CD⊥AB交AB于点D.若cos∠BCD=$\frac{3}{5}$,AC=4,则BC的长为( )| A. | 1 | B. | $\frac{16}{3}$ | C. | 3 | D. | $\frac{20}{3}$ |
9. 二次函数y=ax2+bx+c的图象如图所示,则在下列说法中,与此函数的系数相关的一元二次方程ax2+bx+c=0的根的情况,说法正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则在下列说法中,与此函数的系数相关的一元二次方程ax2+bx+c=0的根的情况,说法正确的是( )
 二次函数y=ax2+bx+c的图象如图所示,则在下列说法中,与此函数的系数相关的一元二次方程ax2+bx+c=0的根的情况,说法正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则在下列说法中,与此函数的系数相关的一元二次方程ax2+bx+c=0的根的情况,说法正确的是( )| A. | 方程有两个相等的实数根 | B. | 方程的实数根的积为负数 | ||
| C. | 方程有两个正的实数根 | D. | 方程没有实数根 |