题目内容

15．若式子$\sqrt{-m}$+$\frac{1}{\sqrt{m+1}}$有意义，则点（m-1，m-2）在第三象限．

分析 二次根式有意义则被开方数大于等于0，分式有意义的条件是分式的分母不为0，从而确定出m的范围，最后可判断出点所在的象限．

解答 解：由二次根式被开方数大于等于0，分式的分母不为0可知：-m≥0，m+1＞0，
解得：m≤0且m＞-1．
∴m-1＜0，m-2＜0．
∴点（m-1，m-2）在第三象限．
故答案为：三．

点评 本题主要考查的是二次根式有意义、分式有意义的条件和点的坐标，掌握二次根式有意义、分式有意义的条件是解题的关键．

练习册系列答案
相关题目
5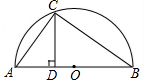．如图是以△ABC的边AB为直径的半圆O，点C恰好在半圆上，过点C作CD⊥AB交AB于点D．若cos∠BCD=$\frac{3}{5}$，AC=4，则BC的长为（　　）
A．1B．$\frac{16}{3}$C．3D．$\frac{20}{3}$
6．∠A和∠C是矩形ABCD的一组对角，则：①∠A与∠C相等；②∠A与∠C互补；③∠A是直角；④∠C是直角，以上结论中，正确的有①②③④．
3．计算：
（1）$\sqrt{24}$×$\sqrt{27}$；
（2）$\sqrt{6}$×（-$\sqrt{15}$）；
（3）$\sqrt{18}$×$\sqrt{20}$×$\sqrt{76}$；
（4）$\sqrt{300}$．
10．若x=$\frac{\sqrt{2}-1}{\sqrt{2}+1}$，y=$\frac{\sqrt{2}+1}{\sqrt{2}-1}$，则xy=1，x+y=6，x-y=-4$\sqrt{2}$，x2+y2=34．
20．计算：
（1）1÷（$\frac{1}{6}$-$\frac{1}{3}$）×$\frac{1}{6}$
（2）-3-[4-（4-3.5×$\frac{1}{3}$）]×[-2+（-3）]
（3）8+（-$\frac{1}{4}$）-5-（-0.25）
（4）99×26
（5）（3.5-7.75-4.25）÷1.1
（6）5$\frac{1}{2}$-（-$\frac{6}{11}$）-[1-$\frac{1}{4}$+（-2）3]×（-2$\frac{2}{3}$）÷$\frac{1}{3}$-[1-（-$\frac{1}{2}$）2]．
6．如图1，△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D，点E在AC边上，连接BE．
（1）若AF是△ABE的中线，且AF=5，AE=6，连结DF，求DF的长；
（2）若AF是△ABE的高，延长AF交BC于点G．
①如图2，若点E是AC边的中点，连结EG，求证：AG+EG=BE；
②如图3，若点E是AC边的动点，连结DF，当点E在AC边上（不含端点）运动时，∠DFG的大小是否改变？如果不变，请求出∠DFG的度数；如果改变，请说明理由．
3．阅读下列文字：
我们知道，对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式．例如由图1可以得到（a+2b）（a+b）=a2+3ab+2b2．

请解答下列问题：
（1）写出图2中所表示的数学等式；
（2）利用（1）中所得到的结论，解决下面的问题：已知a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值；
（3）图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片，请利用所给的纸片拼出一个长方形，使它的面积为2a2+5ab+2b2，把拼出的图形画在方框内，并拼出的图形将多项式2a2+5ab+2b2分解因式．
4．在平面直角坐标系中，点（-4，a2+2）一定在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网