题目内容
17.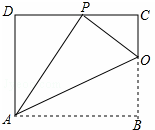 已知:如图,矩形ABCD的一条边AB=10,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕为AO.
已知:如图,矩形ABCD的一条边AB=10,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕为AO.(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1:4,求边AD的长.
分析 (1)根据两角对应相等的两个三角形相似即可判定.
(2)根据相似三角形的性质面积比等于相似比的平方,得到AD=2PC,设PC=x,则AD=2x,在RT△ADP中利用勾股定理即可解决问题.
解答 (1)证明:∵四边形ABCD是矩形,
∴AD=BC,DC=AB,∠DAB=∠B=∠C=∠D=90°,
由折叠可得:AP=AB,PO=BO,∠PAO=∠BAO,∠APO=∠B,
∴∠APO=90°,
∴∠APD=90°-∠CPO=∠POC,
∵∠D=∠C,∠APD=∠POC,
∴△OCP∽△PDA.
(2)解:∵△OCP与△PDA的面积比为1:4,
∴$\frac{CP}{DA}$=$\sqrt{\frac{1}{4}}$=$\frac{1}{2}$,
∴DA=2CP.设PC=x,则AD=2x,PD=10-x,AP=AB=10,
在Rt△PDA中,∵∠D=90°,PD 2+AD2=AP2,
∴(10-x)2+(2x)2=102,
解得:x=4,
∴AD=2x=8.
点评 本题考查相似三角形的判定和性质、矩形的性质、翻折变换、勾股定理等知识,解题的关键是熟练掌握相似三角形的判定,学会用方程的思想解决数学问题,属于中考常考题型.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
8.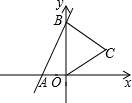 如图,直线y=2x+4与x,y轴分别交于点A,B,以OB为底边在y轴右侧作等腰△OBC,将点C向左平移4个单位,使其对应点C′恰好落在直线AB上,则点C的坐标为( )
如图,直线y=2x+4与x,y轴分别交于点A,B,以OB为底边在y轴右侧作等腰△OBC,将点C向左平移4个单位,使其对应点C′恰好落在直线AB上,则点C的坐标为( )
 如图,直线y=2x+4与x,y轴分别交于点A,B,以OB为底边在y轴右侧作等腰△OBC,将点C向左平移4个单位,使其对应点C′恰好落在直线AB上,则点C的坐标为( )
如图,直线y=2x+4与x,y轴分别交于点A,B,以OB为底边在y轴右侧作等腰△OBC,将点C向左平移4个单位,使其对应点C′恰好落在直线AB上,则点C的坐标为( )| A. | (5,2) | B. | (4,2) | C. | (3,2) | D. | (-1,2) |
5.把直线y=-x-3向上平移m个单位后,与直线y=2x+4的交点在第二象限,则m可以取得的整数值有( )
| A. | 1个 | B. | 3个 | C. | 4个 | D. | 5个 |
9.下列各数中,是无理数的是( )
| A. | cos30° | B. | (-π)0 | C. | -$\frac{1}{3}$ | D. | $\sqrt{64}$ |