题目内容
20. 如图,将?ABCD的边AB延长至点E,使AB=BE,连接BD、DE、EC,DE交BC于点O.
如图,将?ABCD的边AB延长至点E,使AB=BE,连接BD、DE、EC,DE交BC于点O.(1)若∠BOD=2∠A,求证:四边形BECD是矩形;
(2)在不添加任何辅助线的情况下,请写出图中所有的全等三角形.
分析 (1)根据平行四边形的性质可得AB∥CD,AB=CD,∠A=∠DCB,再由AB=BE,可得CD=EB,进而可判定四边形BECD是平行四边形,然后再证明BC=DE即可得到四边形BECD是矩形;
(2)根据平行四边形对边相等可得AD=BC,AB=CD=BE,BD=CE,根据平行四边形对角线互相平分可得BO=CO,DO=EO,再利用SSS可证明三角形全等.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠A=∠DCB,
∵AB=BE,
∴CD=EB,
∴四边形BECD是平行四边形,
∴BO=CO,EO=DO,
∵∠BOD=2∠A,
∴∠BOD=2∠DCO,
∴∠DCO=∠ODC,
∴DO=CO,
∴DE=BC,
∴四边形BECD是矩形;
(2)解:△ABD≌△CDB,△CBD≌△BCE,△ABD≌△EBC,△BOD≌△COE,△BOE≌△COD.△EBD≌△DCE.
点评 此题主要考查了平行四边形的性质,矩形的判定,关键是掌握平行四边形的性质:①边:平行四边形的对边相等.②角:平行四边形的对角相等.③对角线:平行四边形的对角线互相平分.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
10.菱形的对角线AC=8cm,BD=6cm,AC、BD相交于点O,则点O到任一边中点的距离为( )
| A. | 2.5cm | B. | 2.4cm | C. | 5cm | D. | 3cm |
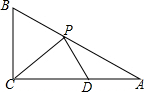 如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=5,点P,D分别是线段AB,AC上的两个动点,则PC+PD的最小值为8.
如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=5,点P,D分别是线段AB,AC上的两个动点,则PC+PD的最小值为8.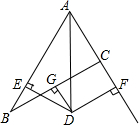 如图,在△ABC中,AB=8,AC=4,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F.
如图,在△ABC中,AB=8,AC=4,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F.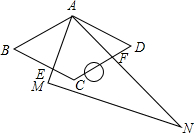 在菱形ABCD中,∠BAD=120°.现将-块含60°角的直角三角尺AMN(其中∠NAM=60°.)叠放在菱形上.然后将三角尺绕点A旋转.在旋转过程中.设AM交边BC于点E,AN交边CD于点F.那么BE+DF与AB有怎样的数量关系?请你通过动手操作.度量、猜想、验证等方法进行探索.
在菱形ABCD中,∠BAD=120°.现将-块含60°角的直角三角尺AMN(其中∠NAM=60°.)叠放在菱形上.然后将三角尺绕点A旋转.在旋转过程中.设AM交边BC于点E,AN交边CD于点F.那么BE+DF与AB有怎样的数量关系?请你通过动手操作.度量、猜想、验证等方法进行探索.