题目内容
11.已知菱形的对角线AC=6,BD=8,则该菱形的周长是20.分析 由菱形ABCD,根据菱形的对角线互相平分且垂直,可得AC⊥BD,OA=OC,OB=OD,易得AB=5;根据菱形的四条边都相等,可得菱形的周长.
解答 解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=$\frac{1}{2}$AC=4,OB=OD=$\frac{1}{2}$BD=3,AB=BC=CD=AD,
∴AB=5,
∴菱形的周长L=20.
故答案为20.
点评 此题考查了菱形的性质:菱形的对角线互相平分且垂直;菱形的四条边都相等.

练习册系列答案
相关题目
16.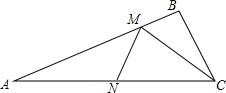 如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
 如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3 |
3.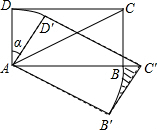 如图,在矩形ABCD中,AB=$\sqrt{3}$,AD=1,把该矩形绕点A顺时针旋转α度得矩形AB′C′D′,点C′落在AB的延长线上,则图中阴影部分的面积是( )
如图,在矩形ABCD中,AB=$\sqrt{3}$,AD=1,把该矩形绕点A顺时针旋转α度得矩形AB′C′D′,点C′落在AB的延长线上,则图中阴影部分的面积是( )
 如图,在矩形ABCD中,AB=$\sqrt{3}$,AD=1,把该矩形绕点A顺时针旋转α度得矩形AB′C′D′,点C′落在AB的延长线上,则图中阴影部分的面积是( )
如图,在矩形ABCD中,AB=$\sqrt{3}$,AD=1,把该矩形绕点A顺时针旋转α度得矩形AB′C′D′,点C′落在AB的延长线上,则图中阴影部分的面积是( )| A. | $\frac{\sqrt{3}}{2}$$-\frac{π}{4}$ | B. | $\frac{\sqrt{3}}{2}-\frac{π}{12}$ | C. | $\frac{\sqrt{3}}{2}-\frac{π}{2}$ | D. | $\frac{\sqrt{3}}{2}-\frac{π}{6}$ |
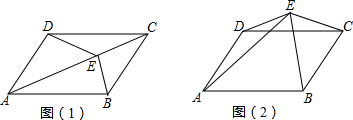
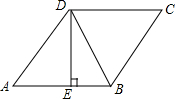 如图,在菱形ABCD中,已知DE⊥AB,AE:AD=3:5,BE=2,则菱形ABCD的面积是20.
如图,在菱形ABCD中,已知DE⊥AB,AE:AD=3:5,BE=2,则菱形ABCD的面积是20. 如图,正方形网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,按下列要求作答:
如图,正方形网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,按下列要求作答: 如图,将?ABCD的边AB延长至点E,使AB=BE,连接BD、DE、EC,DE交BC于点O.
如图,将?ABCD的边AB延长至点E,使AB=BE,连接BD、DE、EC,DE交BC于点O. 如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点,且OE=2,则菱形ABCD的边长为4.
如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点,且OE=2,则菱形ABCD的边长为4.