题目内容
10．菱形的对角线AC=8cm，BD=6cm，AC、BD相交于点O，则点O到任一边中点的距离为（ ）| A． | 2.5cm | B． | 2.4cm | C． | 5cm | D． | 3cm |
分析 根据菱形的对角线互相垂直且平分可得出直角△BOC中，从而利用勾股定理得出BC的长，然后利用菱形的面积解答即可．
解答 解：∵ABCD是菱形，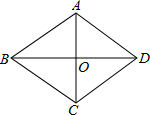
∴OA=OC，OB=OD，OB⊥OC，
又∵AC=8cm，BD=6cm，
∴OA=OC=4cm，OB=OD=3cm，
在直角△BOC中，
由勾股定理，得BC=$\sqrt{{3}^{2}+{4}^{2}}$=5cm，
所以菱形的面积=$\frac{1}{2}×AC×BD=BC×高$，
可得：高=$\frac{1}{2}×6×8÷5=4.8$，
所以点O到任一边中点的距离为2.4，
故选B
点评 本题考查了菱形的性质，需要用到菱形的对角线互相垂直且平分，菱形的面积公式是解题关键．
练习册系列答案
相关题目
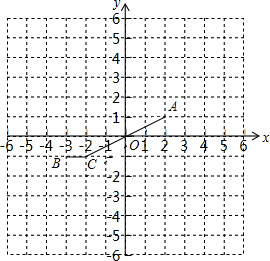若A、B、C、D四点构成平行四边形A（2，1）、B（-3，1）、C（-2，-1），则顶点D的坐标为（3，1）或（1，1）或（-5，-3）．
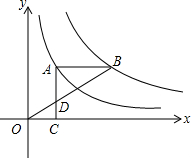如图，点A在双曲线y=$\frac{2}{x}$上，点B在双曲线y=$\frac{k}{x}$（k≠0）上，AB∥x轴，过点A作AC⊥x轴于C．连接OB与AC相交于点D，若AD=2DC．则k的值为6．
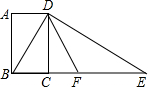如图，四边形ABCD为矩形，过点D作对角线BD的垂线，交BC的延长线于点E，取BE的中点F，连接DF，DF=3．设AB=x，AD=y，则x2+（y-3）2的值为9．
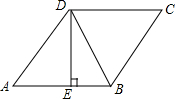如图，在菱形ABCD中，已知DE⊥AB，AE：AD=3：5，BE=2，则菱形ABCD的面积是20．
如图，将?ABCD的边AB延长至点E，使AB=BE，连接BD、DE、EC，DE交BC于点O．