题目内容
10.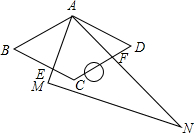 在菱形ABCD中,∠BAD=120°.现将-块含60°角的直角三角尺AMN(其中∠NAM=60°.)叠放在菱形上.然后将三角尺绕点A旋转.在旋转过程中.设AM交边BC于点E,AN交边CD于点F.那么BE+DF与AB有怎样的数量关系?请你通过动手操作.度量、猜想、验证等方法进行探索.
在菱形ABCD中,∠BAD=120°.现将-块含60°角的直角三角尺AMN(其中∠NAM=60°.)叠放在菱形上.然后将三角尺绕点A旋转.在旋转过程中.设AM交边BC于点E,AN交边CD于点F.那么BE+DF与AB有怎样的数量关系?请你通过动手操作.度量、猜想、验证等方法进行探索.
分析 首先连接AC,由在菱形ABCD中,∠BAD=60°,使三角尺60°角的顶点与点A重合,易证得ABC、△ACD都是等边三角形,继而证得△△BAE≌△CAF,则可证得结论.
解答 解:BE+DF=AB.
理由:连接AC.
∵四边形ABCD是菱形,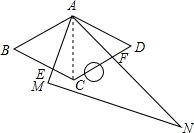 ∠BAD=120°,
∠BAD=120°,
∴AB=BC=CD=DA,∠B=∠D=60°,
∴△ABC、△ACD都是等边三角形,
∴AB=AC,∠BAC=∠ACD=∠B=60°.
∵∠EAF=60°,
∴∠BAC=∠EAF=60°,
∴∠BAC-∠EAC=∠EAF-∠EAC,
即∠BAE=∠CAF,
在△BAE和△CAF中,
$\left\{\begin{array}{l}{∠BAE=∠CAF}\\{AB=AC}\\{∠B=∠ACF}\end{array}\right.$,
∴△BAE≌△CAF(ASA),
∴BE=CF,
∴BE+DF=CF+DF=CD=AB.
点评 此题考查了菱形的性质、等边三角形的判定与性质以及全等三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
 如图,将?ABCD的边AB延长至点E,使AB=BE,连接BD、DE、EC,DE交BC于点O.
如图,将?ABCD的边AB延长至点E,使AB=BE,连接BD、DE、EC,DE交BC于点O. 如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点,且OE=2,则菱形ABCD的边长为4.
如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点,且OE=2,则菱形ABCD的边长为4.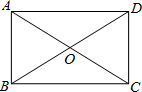 如图,矩形ABCD中,对角线AC和BD相交于点0,OD=AD,则sin∠OBA=$\frac{1}{2}$.
如图,矩形ABCD中,对角线AC和BD相交于点0,OD=AD,则sin∠OBA=$\frac{1}{2}$.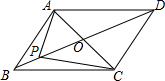 如图,已知四边形ABCD是平行四边形,点O为对角线AC、BD的交点
如图,已知四边形ABCD是平行四边形,点O为对角线AC、BD的交点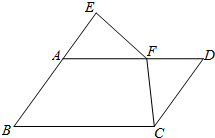 如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在AD边上,且AE=DF,AF=CD.求证:FE=FC.
如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在AD边上,且AE=DF,AF=CD.求证:FE=FC.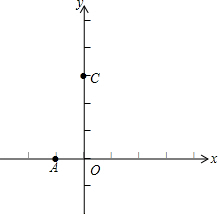 在平面直角坐标系xOy(如图)中,经过点A(-1,0)的抛物线y=-x2+bx+3与y轴交于点C,点B与点A、点D与点C分别关于该抛物线的对称轴对称.
在平面直角坐标系xOy(如图)中,经过点A(-1,0)的抛物线y=-x2+bx+3与y轴交于点C,点B与点A、点D与点C分别关于该抛物线的对称轴对称.