题目内容
16.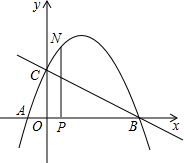 如图,抛物线与x轴交于点A(-$\frac{1}{3}$,0),点B(2,0),与y轴交于点C(0,1),连接BC.
如图,抛物线与x轴交于点A(-$\frac{1}{3}$,0),点B(2,0),与y轴交于点C(0,1),连接BC.(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(-$\frac{1}{3}<t<2$),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.
分析 (1)可设抛物线的解析式为y=ax2+bx+c,然后只需运用待定系数法就可解决问题;
(2)当-$\frac{1}{3}$<t<2时,点N在x轴的上方,则NP等于点N的纵坐标,只需求出AB,就可得到S与t的函数关系式;
(3)根据相似三角形的性质可得PN=2PO.由于PO=|t|,根据0<t<2,由PN=2PO得到关于t的方程,解这个方程,就可解决问题.
解答 解:(1)设抛物线的解析式为y=ax2+bx+c,由题意可得:$\left\{\begin{array}{l}{\frac{1}{9}a-\frac{1}{3}b+c=0}\\{4a+2b+c=0}\\{c=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{3}{2}}\\{b=\frac{5}{2}}\\{c=1}\end{array}\right.$.
∴抛物线的函数关系式为y=-$\frac{3}{2}$x2+$\frac{5}{2}$x+1;
(2)当-$\frac{1}{3}$<t<2时,yN>0,
∴NP=|yN|=yN=-$\frac{3}{2}$t2+$\frac{5}{2}$t+1,
∴S=$\frac{1}{2}$AB•PN
=$\frac{1}{2}$×(2+$\frac{1}{3}$)×(-$\frac{3}{2}$t2+$\frac{5}{2}$t+1)
=$\frac{7}{6}$(-$\frac{3}{2}$t2+$\frac{5}{2}$t+1)
=-$\frac{7}{4}$t2+$\frac{35}{12}$t+$\frac{7}{6}$;
(3)∵△OPN∽△COB,
∴$\frac{PO}{OC}$=$\frac{PN}{OB}$,
∴$\frac{PO}{1}$=$\frac{PN}{2}$,
∴PN=2PO.
当0<t<2时,PN=|yN|=yN=-$\frac{3}{2}$t2+$\frac{5}{2}$t+1,PO=|t|=t,
∴-$\frac{3}{2}$t2+$\frac{5}{2}$t+1=2t,
整理得:3t2-t-2=0,
解得:t3=-$\frac{2}{3}$,t4=1.
∵-$\frac{2}{3}$<0,0<1<2,
∴t=1,此时点N的坐标为(1,2).
故点N的坐标为(1,2).
点评 本题主要考查了二次函数综合题,解题的关键是熟悉待定系数法求二次函数的解析式、相似三角形的性质、解一元二次方程等知识,需要注意的是:用点的坐标表示相关线段的长度时,应先用坐标的绝对值表示线段的长度,然后根据坐标的正负去绝对值;解方程后要检验,不符合条件的解要舍去.

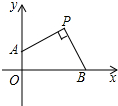 如图,已知P(2,2),点B、A分别在x轴正半轴和y轴正半轴上,∠APB=90°,则OA+OB=4.
如图,已知P(2,2),点B、A分别在x轴正半轴和y轴正半轴上,∠APB=90°,则OA+OB=4. 已知.如图,在正方形(四边相等,四个内角都为90°)ABCD中,过顶点D作射线交AB于E,过点B作BF⊥DE,F为垂足,联结AF,过点A作AG⊥AF交DE于G.求证:∠AGD=135°.
已知.如图,在正方形(四边相等,四个内角都为90°)ABCD中,过顶点D作射线交AB于E,过点B作BF⊥DE,F为垂足,联结AF,过点A作AG⊥AF交DE于G.求证:∠AGD=135°.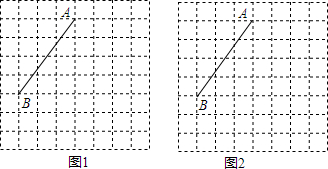
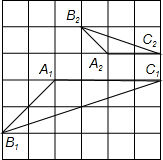 学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”.那么你认为△A1B1C1和△A2B2C2相似.(填相似或不相似);理由是$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$.
学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”.那么你认为△A1B1C1和△A2B2C2相似.(填相似或不相似);理由是$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$.