题目内容
11.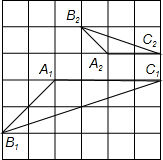 学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”.那么你认为△A1B1C1和△A2B2C2相似.(填相似或不相似);理由是$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$.
学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”.那么你认为△A1B1C1和△A2B2C2相似.(填相似或不相似);理由是$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$.
分析 由勾股定理求出A1B1=2$\sqrt{2}$,B1C1=2$\sqrt{10}$,A2B2=$\sqrt{2}$,B2C2=$\sqrt{10}$,证出$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$=2,由三边成比例的两个三角形相似即可得出结论.
解答 解:由题意得:A1C1=4,A2C2=2,
由勾股定理得:A1B1=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,B1C1=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$,
A2B2=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,B2C2=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{2\sqrt{2}}{\sqrt{2}}$=2,$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=$\frac{2\sqrt{10}}{\sqrt{10}}$=2,$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$=$\frac{4}{2}$=2,
∴$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$=2,
∴△A1B1C1∽△A2B2C2.
故答案为:相似,$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$.
点评 本题考查了相似三角形的判定方法、勾股定理;熟练掌握勾股定理,熟记三边成比例的两个三角形相似是解决问题的关键.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案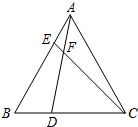 在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.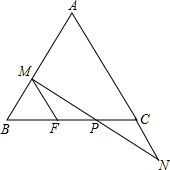 在△ABC中,AB=AC,P是BC边上的一点,过P引直线分别交AB于M,交AC的延长线于N,且PM=PN,MF∥AN.
在△ABC中,AB=AC,P是BC边上的一点,过P引直线分别交AB于M,交AC的延长线于N,且PM=PN,MF∥AN.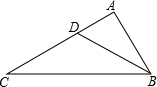 如图,点D是△ABC的边AC的上一点,且∠ABD=∠C;如果$\frac{AD}{CD}$=$\frac{1}{2}$,那么$\frac{BD}{BC}$=$\frac{\sqrt{3}}{3}$.
如图,点D是△ABC的边AC的上一点,且∠ABD=∠C;如果$\frac{AD}{CD}$=$\frac{1}{2}$,那么$\frac{BD}{BC}$=$\frac{\sqrt{3}}{3}$. 如图,抛物线与x轴交于点A(-$\frac{1}{3}$,0),点B(2,0),与y轴交于点C(0,1),连接BC.
如图,抛物线与x轴交于点A(-$\frac{1}{3}$,0),点B(2,0),与y轴交于点C(0,1),连接BC. 在平面直角坐标系中,已知点A(1,0),B(2,2),请在图中画出线段AB,并画出线段AB绕点O顺时针旋转90°后的图形.
在平面直角坐标系中,已知点A(1,0),B(2,2),请在图中画出线段AB,并画出线段AB绕点O顺时针旋转90°后的图形.