题目内容
4.若2|a+b-1|与$\frac{1}{3}$(a-b-3)2互为相反数,则[-3a2(ab2+2a)+4a(-ab)2]÷(-4a)的值是5.分析 先根据非负数的性质求出a、b,然后化简后代入即可.
解答 解:∵2|a+b-1|与$\frac{1}{3}$(a-b-3)2互为相反数,
∴2|a+b-1|+$\frac{1}{3}$(a-b-3)2=0,
∵2|a+b-1|≥0,$\frac{1}{3}$(a-b-3)2≥0,
则有$\left\{\begin{array}{l}{a+b=1}\\{a-b=3}\end{array}\right.$解得$\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$,
∴原式=(-3a3b2-6a3+4a3b2)÷(-4a)
=(a3b2-6a3)÷(-4a)
=-$\frac{1}{4}$a2b2+$\frac{3}{2}$a2
=-$\frac{1}{4}$×4×1+6
=5.
故答案为5.
点评 本题考查非负数的性质、整式的混合运算法则、正确运用法则是解题的关键.

练习册系列答案
相关题目
16.△ABC中,∠A:∠B:∠C=2:3:4,则∠A的度数为( )
| A. | 35° | B. | 40° | C. | 70° | D. | 110° |
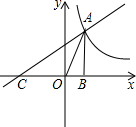 如图,在平面直角坐标系中,直线$y=x+\frac{k}{2}$与双曲线$y=\frac{k}{x}$在第一象限交于点A,与x轴交于点C,AB⊥x轴,垂足为B,此时点B(1,0).求:
如图,在平面直角坐标系中,直线$y=x+\frac{k}{2}$与双曲线$y=\frac{k}{x}$在第一象限交于点A,与x轴交于点C,AB⊥x轴,垂足为B,此时点B(1,0).求: 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列由5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1).其中正确的结论有①③④⑤.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列由5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1).其中正确的结论有①③④⑤.