题目内容
19.一次函数y=kx+b的图象不经过第一象限,与x轴,y轴分别交于A,B两点,如果b是方程x2+2x+$\sqrt{3{x}^{2}+6x-5}$=5的解,且OA:OB=2:1(1)求b;
(2)求一次函数解析式.
分析 (1)解方程求得x=-3,即可求得b=-3,
(2)根据OA:OB=2:1,得出A(-6,0),代入y=kx-3中,根据待定系数法即可求得.
解答 解:(1)∵方程x2+2x+$\sqrt{3{x}^{2}+6x-5}$=5,
∴设x2+2x=y,则y+$\sqrt{3y-5}$=5,
化成整式方程为y2-13y+30=0,
解得y=10或3,
经检验y=3是原方程的解,
解x2+2x=3得x1=-3,x2=1,
∵一次函数y=kx+b的图象不经过第一象限,
∴b<0,
∴b=-3;
(2)∵OA:OB=2:1,OB=3,
∴OA=6,
∴A(-6,0),
代入y=kx-3得,0=-6k-3,解得k=-$\frac{1}{2}$,
∴一次函数解析式为y=-$\frac{1}{2}$x-3.
点评 本题考查了一次函数的性质和待定系数法求一次函数的解析式,求得b的值是解题的关键.

练习册系列答案
相关题目
7. 如图,已知l1∥l2,且∠1=120°,则∠2=( )
如图,已知l1∥l2,且∠1=120°,则∠2=( )
 如图,已知l1∥l2,且∠1=120°,则∠2=( )
如图,已知l1∥l2,且∠1=120°,则∠2=( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
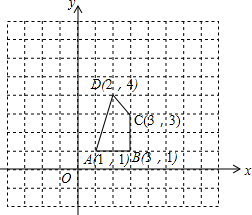 将图中的四边形作下列运动,画出相应的图形,并写出各个顶点的坐标;
将图中的四边形作下列运动,画出相应的图形,并写出各个顶点的坐标;