题目内容
13.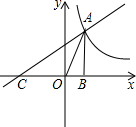 如图,在平面直角坐标系中,直线$y=x+\frac{k}{2}$与双曲线$y=\frac{k}{x}$在第一象限交于点A,与x轴交于点C,AB⊥x轴,垂足为B,此时点B(1,0).求:
如图,在平面直角坐标系中,直线$y=x+\frac{k}{2}$与双曲线$y=\frac{k}{x}$在第一象限交于点A,与x轴交于点C,AB⊥x轴,垂足为B,此时点B(1,0).求:(1)求两个函数解析式;
(2)求△AOC的周长.
分析 (1)根据点B(1,0)即可求得A横坐标,代入$y=x+\frac{k}{2}$与$y=\frac{k}{x}$从而求得两个函数的解析式;
(2)根据直线的解析式求得点C的坐标,根据点A的坐标,从而求得三角形的面积.
解答 解:(1)∵点B(1,0).
∴A点横坐标为1,
代入$y=x+\frac{k}{2}$得纵坐标为y=1+$\frac{k}{2}$,
∴A(1,1+$\frac{k}{2}$),
代入$y=\frac{k}{x}$得k=1+$\frac{k}{2}$,
∴k=2,
一次函数解析式y=x+1,
反比例函数解析式y=$\frac{2}{x}$;
(2)在直线y=x+1中,令y=0,则x=-1,
∴C点坐标(-1,0),
∵A(1,2),
∴S△AOC=$\frac{1}{2}$×1×2=1.
点评 本题考查了反比例函数和一次函数的交点,交点坐标符合两个解析式是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
1.若二次函数y=ax2的图象经过点(-2.-4),则a的值为( )
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
16.在-3,-(-3),|-3|,(-3)2,(-3)3,-33中,负数的个数有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
