题目内容
12.平行四边形的两邻边的比是2:5,周长为28cm,求平行四边形的各边的长.分析 根据平行四边形的性质可知:邻边之和为周长的一半,可设较短的边为2x,则较长的为5x,根据题意列方程即可求出.
解答 解:根据平行四边形的性质可知:邻边之和为周长的一半,
设较短的边为2x,则较长的为5x,
∴2x+5x=14,
∴x=2,
∴5x=5×2=10,2x=2×2=4,
∴平行四边形的各边的长分别为10cm、4cm、10cm、4cm.
点评 本题主要考查了平行四边形的对边相等的性质及周长计算;熟记平行四边形的两邻边之和为周长的一半是解决问题的关键.

练习册系列答案
相关题目
20.已知a,b满足等式M=a2+b2+20,N=4(2b-a),则M,N的大小关系是( )
| A. | M>N | B. | M<N | C. | M=N | D. | 以上都不对 |
7. 如图,已知l1∥l2,且∠1=120°,则∠2=( )
如图,已知l1∥l2,且∠1=120°,则∠2=( )
 如图,已知l1∥l2,且∠1=120°,则∠2=( )
如图,已知l1∥l2,且∠1=120°,则∠2=( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
1.若二次函数y=ax2的图象经过点(-2.-4),则a的值为( )
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
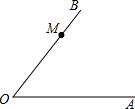 如图,已知∠AOB,点M为OB上一点.
如图,已知∠AOB,点M为OB上一点.