题目内容
14.化简下列各式:(1)(x-1)2(x+1)2-1;
(2)$\frac{{x}^{2}-8x+16}{{x}^{2}+2x}$÷($\frac{12}{x+2}$-x+2)+$\frac{1}{x+4}$.
分析 (1)根据平方差公式进行计算即可;
(2)先对式子能分解因式的先分解因式,对括号内的先通分再相加,然后化简即可.
解答 解:(1)(x-1)2(x+1)2-1
=[(x-1)(x+1)]2-1
=(x2-1)2-1
=x4-2x2+1-1
=x4-2x2;
(2)$\frac{{x}^{2}-8x+16}{{x}^{2}+2x}$÷($\frac{12}{x+2}$-x+2)+$\frac{1}{x+4}$
=$\frac{(x-4)^{2}}{x(x+2)}÷\frac{12-(x-2)(x+2)}{x+2}+\frac{1}{x+4}$
=$\frac{(x-4)^{2}}{x(x+2)}×\frac{x+2}{12-{x}^{2}+4}+\frac{1}{x+4}$
=$\frac{(x-4)^{2}}{x(x+2)}×\frac{x+2}{(4+x)(4-x)}+\frac{1}{x+4}$
=$-\frac{x-4}{x(x+4)}+\frac{1}{x+4}$
=$\frac{4-x+x}{x(x+4)}$
=$\frac{4}{x(x+4)}$
=$\frac{4}{{x}^{2}+4x}$.
点评 本题考查分式的混合运算、整式的混合运算、平方差公式、完全平方差公式、因式分解,考查的是对问题观察与巧妙利用公式的能力,主要是采用因式分解的数学思想对所化简的式子进行分解因式后再化简.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
5.已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
| A. | 24cm和12cm | B. | 16cm和22cm | C. | 20cm和16cm | D. | 22cm和16cm |
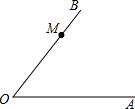 如图,已知∠AOB,点M为OB上一点.
如图,已知∠AOB,点M为OB上一点.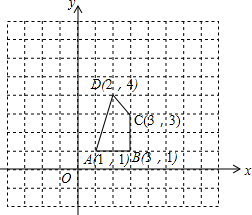 将图中的四边形作下列运动,画出相应的图形,并写出各个顶点的坐标;
将图中的四边形作下列运动,画出相应的图形,并写出各个顶点的坐标;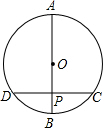 如图,⊙O的直径AB垂直弦CD于点P,且P是半径OB的中点,若CD=6cm,则⊙O的半径长为2$\sqrt{3}$cm.
如图,⊙O的直径AB垂直弦CD于点P,且P是半径OB的中点,若CD=6cm,则⊙O的半径长为2$\sqrt{3}$cm.