题目内容
9.已知(m-n)2=8,(m+n)2=2,求m2+n2的值.分析 由完全平方公式可知:(m-n)2展开含+2mn,而(m+n)2展开含-2mn,二者相加只剩下m2+n2的倍数,从而得出结论.
解答 解:∵(m-n)2+(m+n)2=m2+n2-2mn+m2+n2+2mn=2(m2+n2)=8+2=10,
∴m2+n2=10÷2=5.
点评 本题考查了完全平方公式的运用,解题的关键是:发现“(m-n)2展开含+2mn,而(m+n)2展开含-2mn,二者相加只剩下m2+n2的倍数”,本题属于基础题,难度不大,但是在解决该类问题时,部分同学利用完全平方公式展开,联立成方程组,从而耽误了做题时间,也极其容易在解方程组中出现错误.

练习册系列答案
相关题目
20.已知a,b满足等式M=a2+b2+20,N=4(2b-a),则M,N的大小关系是( )
| A. | M>N | B. | M<N | C. | M=N | D. | 以上都不对 |
1.若二次函数y=ax2的图象经过点(-2.-4),则a的值为( )
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
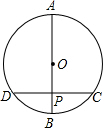 如图,⊙O的直径AB垂直弦CD于点P,且P是半径OB的中点,若CD=6cm,则⊙O的半径长为2$\sqrt{3}$cm.
如图,⊙O的直径AB垂直弦CD于点P,且P是半径OB的中点,若CD=6cm,则⊙O的半径长为2$\sqrt{3}$cm.