题目内容
6.如果|3x+2y+5|+(2x-7y-15)2=0,则x-y的值是$\left\{\begin{array}{l}{x=-\frac{1}{5}}\\{y=-\frac{11}{5}}\end{array}\right.$.分析 利用非负数的性质列出方程组,求出方程组的解得到x与y的值,即可求出x-y的值.
解答 解:∵|3x+2y+5|+(2x-7y-15)2=0,
∴$\left\{\begin{array}{l}{3x+2y=-5①}\\{2x-7y=15②}\end{array}\right.$,
①×7+②×2得:25x=-5,
解得:x=-$\frac{1}{5}$,
把x=-$\frac{1}{5}$代入①得:y=-$\frac{11}{5}$,
则方程组的解为$\left\{\begin{array}{l}{x=-\frac{1}{5}}\\{y=-\frac{11}{5}}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{x=-\frac{1}{5}}\\{y=-\frac{11}{5}}\end{array}\right.$
点评 此题考查了解二元一次方程组,以及非负数的性质:绝对值与偶次幂,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
16.一个自然数的算术平方根是a,那么与这个自然数相邻的下一个自然数的平方根是( )
| A. | a+1 | B. | ±$\sqrt{a+1}$ | C. | a2+1 | D. | ±$\sqrt{{a}^{2}+1}$ |
18.小红制作了十张卡片,上面分别标有0~9这十个数字.从这十张卡片中随机抽取一张恰好能被3整除的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{2}{5}$ |
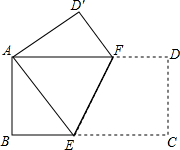 如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,
如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,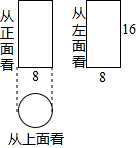 如图是一个几何体从三个方向看所得到的形状图,则该几何体的表面积为160π(结果保留π)
如图是一个几何体从三个方向看所得到的形状图,则该几何体的表面积为160π(结果保留π)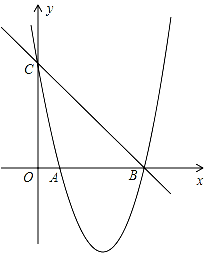 如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).