Question

14．在△ABC中，sinA=$\frac{1}{2}$，AB=8，BC=6，则AC=$2\sqrt{5}+4\sqrt{3}或4\sqrt{3}-2\sqrt{5}$．

Answer 1

分析 分∠C为锐角和∠C为钝角两种情况，先在Rt△ABD中，求得BD=ABsinA=4、AD=$\sqrt{A{B}^{2}-A{D}^{2}}$=4$\sqrt{3}$，再在Rt△BCD中，求得CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=2$\sqrt{5}$，结合图象可得答案．

解答 解：①当∠C为锐角时，如图1，

过点B作BD⊥AC于点D，
在Rt△ABD中，∵BD=ABsinA=8×$\frac{1}{2}$=4，
∴AD=$\sqrt{A{B}^{2}-A{D}^{2}}$=4$\sqrt{3}$，
在Rt△BCD中，∵CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$，
∴AC=AD+CD=4$\sqrt{3}+$2$\sqrt{5}$；
②当∠C为钝角时，如图2，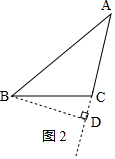

过点B作BD⊥AC，交AC延长线于点D，
此时AC=AD-CD=4$\sqrt{3}$-2$\sqrt{5}$，
故答案为：$2\sqrt{5}+4\sqrt{3}或4\sqrt{3}-2\sqrt{5}$．

点评 本题主要考查解直角三角形，熟练掌握三角函数的定义与勾股定理及分类讨论思想是解题的关键．