题目内容
11.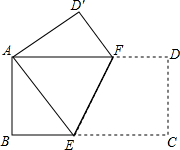 如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,
如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,求(1)AE的长.
(2)折痕EF的长.
分析 (1)根据折叠的性质得到AE=CE,根据勾股定理即可得到结论
(2)先过点F作FG⊥BC于G.利用勾股定理可求出AE,再利用翻折变换的知识,可得到AE=CE,∠AEF=∠CEF,再利用平行线可得∠AEF=∠AFE,故有AE=AF.求出EG,再次使用勾股定理可求出EF的长.
解答 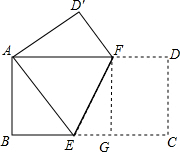 解:(1)∵将长方形纸片ABCD折叠,使C点与A点重合,
解:(1)∵将长方形纸片ABCD折叠,使C点与A点重合,
∴AE=CE,
∴BE=BC-CE=BC-AE=8-AE,
∵∠B=90°,
∴AB2+BE2=AE2,
即42+(8-AE)2=AE2,
∴AE=5;
(2)解:过点F作FG⊥BC于G
∵EF是直角梯形AECD的折痕
∴AE=CE,∠AEF=∠CEF.
又∵AD∥BC
∴∠AEF=∠AFE.
∴AE=AF.
在Rt△ABE中,
设BE=x,AB=4,AE=CE=8-x.x2+42=(8-x)2,
解得x=3.
在Rt△FEG中,EG=BG-BE=AF-BE=AE-BE=5-3=2,FG=4,
∴EF=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$.
点评 本题考查了翻折变换,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列命题是假命题的是( )
| A. | ±$\frac{1}{5}$是$\frac{1}{25}$的平方根 | B. | 81的平方根是9 | ||
| C. | 0.04的算术平方根是0.2 | D. | -27的立方根是-3 |
 如图,反比例函数y=$\frac{3}{x}$的图象与一次函数y=x+2的图象交于A、B两点.
如图,反比例函数y=$\frac{3}{x}$的图象与一次函数y=x+2的图象交于A、B两点.
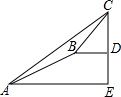 这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5$\sqrt{5}$米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5$\sqrt{5}$米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )