题目内容
一个不透明的袋子中装有三个完全相同的小球,小球上分别标有数字3,4,5,从袋中随机取出一个小球,用小球上的数字作十位,然后放回,搅匀后再取出一个小球,用小球上的数字作个位,这样组成一个两位数;试问:按这种方法能组成哪些两位数?十位上的数字与个位上的数字之和为8的两位数的概率是多少?用列表法或画树状图加以说明.
考点:列表法与树状图法
专题:
分析:先利用树状图展示所有9种等可能的结果数,即组成的两位数为33,34,35,43,44,45,53,54,55;其中十位上的数字与个位上的数字之和为8的两位数有44、35和53三个,然后根据概率的概念计算即可.
解答:解:列表得:
共有9种等可能的结果数,即按这种方法能组成的两位数有33,34,35,43,44,45,53,54,55;
其中十位上的数字与个位上的数字之和为8的两位数有44、35和53三个,
∴P(十位与个位数字之和为8)=
=
.
| 3 | 4 | 5 | |
| 3 | 33 | 34 | 35 |
| 4 | 43 | 44 | 45 |
| 5 | 53 | 54 | 55 |
其中十位上的数字与个位上的数字之和为8的两位数有44、35和53三个,
∴P(十位与个位数字之和为8)=
| 3 |
| 9 |
| 1 |
| 3 |
点评:本题考查了利用列表法与树形图法求概率的方法:先利用列表法或树形图法展示所有等可能的结果数n,然后找出其中某事件所占有的结果数m,则根据概率的概念得到这个事件的概率=
.
| m |
| n |

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 如图,正方形网格中的每个小正方形边长都是1.已知A、B是两格点,若△ABC为等腰三角形,且S△ABC=1.5,则满足条件的格点C有( )
如图,正方形网格中的每个小正方形边长都是1.已知A、B是两格点,若△ABC为等腰三角形,且S△ABC=1.5,则满足条件的格点C有( )| A、1个 | B、2个 | C、3个 | D、4个 |
已知反比例函数y=(m-1)xm2-2,当x>0时,y随x的增大而增大,则m的值为( )
| A、1 | B、-1 | C、±1 | D、2 |
 如图,△ABC内接于半径为5的⊙O,圆心O到弦BC的距离等于3,则cosA等于( )
如图,△ABC内接于半径为5的⊙O,圆心O到弦BC的距离等于3,则cosA等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在△ABC中,AD是BC边上的高,AC=3
如图,在△ABC中,AD是BC边上的高,AC=3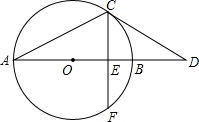 如图,AB为圆O的直径,点C在圆O上,过点C作圆O的切线交AB的延长线于点D,已知∠D=30°.
如图,AB为圆O的直径,点C在圆O上,过点C作圆O的切线交AB的延长线于点D,已知∠D=30°. 某学校要成立一支由6名女生组成的礼仪队,初三两个班各选6名女生,分别组成甲队和乙队参加选拔,每位女生的身高(米)统计如图,部分统计量如下表:
某学校要成立一支由6名女生组成的礼仪队,初三两个班各选6名女生,分别组成甲队和乙队参加选拔,每位女生的身高(米)统计如图,部分统计量如下表: 如图:
如图: