Question

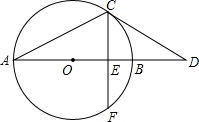如图，AB为圆O的直径，点C在圆O上，过点C作圆O的切线交AB的延长线于点D，已知∠D=30°．
（1）求∠A的度数；
（2）若点F在圆O上，CF⊥AB，垂足为E，CF=4

3

，求弧CB与线段CE及EB所围成图形的面积．

Answer 1

考点：切线的性质,扇形面积的计算

专题：计算题

分析：（1）连接OC，如图，根据切线的性质得OC⊥CD，而∠D=30°，根据互余得到∠COB=60°，然后根据圆周角得到计算∠A的度数；
（2）根据垂径定理．由CF⊥直径AB得到CE=

1

2

CF=2

3

，在Rt△OCE中利用含30度的直角三角形三边的关系得OE=

3

3

CE=2，OC=2OE=4，然后根据扇形面积公式和弧CB与线段CE及EB所围成图形的面积=S_扇形BOC-S_△OCE进行计算即可．

解答：解：（1）连接OC，如图，
∵CD为⊙O的切线，
∴OC⊥CD，
∵∠D=30°，
∴∠COB=60°，
∴∠A=

1

2

∠COB=30°；
（2）∵CF⊥直径AB，
∴CE=EF，
∴CE=

1

2

CF=2

3

，
在Rt△OCE中，∵∠COE=60°，
∴OE=

3

3

CE=2，
OC=2OE=4，
∴弧CB与线段CE及EB所围成图形的面积
=S_扇形BOC-S_△OCE
=

60•π•42

360

-

1

2

×2×2

3

=

8

3

π-2

3

．

点评：本题考查了切线的性质：圆的切线垂直于经过切点的半径．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．也考查了含30度的直角三角形三边的关系和扇形的面积公式．