题目内容
16.化简:①($\frac{2x}{x-3}$$-\frac{x}{x+3}$)•$\frac{{x}^{2}-9}{x}$
②$\frac{x-2}{{x}^{2}-2x+1}$÷($\frac{2x-1}{x-1}$-x-1)-$\frac{1}{x}$
③先化简,再求代数式$\frac{{x}^{2}}{{x}^{2}+4x+4}$÷$\frac{x}{x+2}$$-\frac{x-1}{x+2}$的值,其中x=$\sqrt{2}$-2.
分析 ①根据分式的减法和乘法可以解答本题;
②根据分式的除法和减法可以解答本题;
③先化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解答 解:①($\frac{2x}{x-3}$$-\frac{x}{x+3}$)•$\frac{{x}^{2}-9}{x}$
=$\frac{2x(x+3)-x(x-3)}{(x+3)(x-3)}•\frac{(x+3)(x-3)}{x}$
=2(x+3)-(x-3)
=2x+6-x+3
=x+9;
②$\frac{x-2}{{x}^{2}-2x+1}$÷($\frac{2x-1}{x-1}$-x-1)-$\frac{1}{x}$
=$\frac{x-2}{(x-1)^{2}}÷\frac{(2x-1)-(x+1)(x-1)}{x-1}-\frac{1}{x}$
=$\frac{x-2}{(x-1)^{2}}•\frac{x-1}{-x(x-2)}-\frac{1}{x}$
=$\frac{1}{x(1-x)}-\frac{1}{x}$
=$\frac{1-(1-x)}{x(1-x)}$
=$\frac{1}{1-x}$;
③$\frac{{x}^{2}}{{x}^{2}+4x+4}$÷$\frac{x}{x+2}$$-\frac{x-1}{x+2}$
=$\frac{{x}^{2}}{(x+2)^{2}}•\frac{x+2}{x}-\frac{x-1}{x+2}$
=$\frac{x}{x+2}-\frac{x-1}{x+2}$
=$\frac{1}{x+2}$,
当x=$\sqrt{2}$-2时,原式=$\frac{1}{\sqrt{2}-2+2}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

 名校课堂系列答案
名校课堂系列答案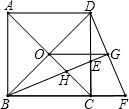 如图,O为正方形ABCD对角线BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG、OC,OC交BG于点H.下面四个结论中不正确的是( )
如图,O为正方形ABCD对角线BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG、OC,OC交BG于点H.下面四个结论中不正确的是( )| A. | △BCE≌△DCF | B. | OG∥AD | C. | BH=GH | D. | OG=$\frac{1}{2}$BD |
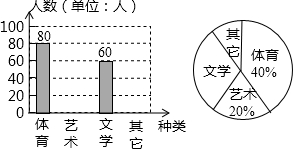 为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题: 请在方格内画△ABC,使它的顶点都在格点上,且三边长分别为$\sqrt{2}$,$\sqrt{10}$,4$\sqrt{\frac{1}{2}}$.
请在方格内画△ABC,使它的顶点都在格点上,且三边长分别为$\sqrt{2}$,$\sqrt{10}$,4$\sqrt{\frac{1}{2}}$.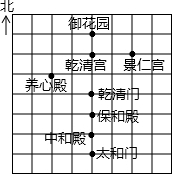 如图所示的是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,且表示保和殿的点的坐标为(1,-4),表示景仁宫的点的坐标为(3,-1),则表示养心殿的点的坐标是(-1,-2).
如图所示的是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,且表示保和殿的点的坐标为(1,-4),表示景仁宫的点的坐标为(3,-1),则表示养心殿的点的坐标是(-1,-2). 如图,矩形的两条对角线夹角为60°,一条短边为3,则矩形的长边长为3$\sqrt{3}$.
如图,矩形的两条对角线夹角为60°,一条短边为3,则矩形的长边长为3$\sqrt{3}$. 在如图所示的4×4方格中,每个小方格的边长都为1
在如图所示的4×4方格中,每个小方格的边长都为1