题目内容
8. 在如图所示的4×4方格中,每个小方格的边长都为1
在如图所示的4×4方格中,每个小方格的边长都为1(1)在图(1)中画出长度为$\sqrt{17}$的线段,要求线段的端点在格点上;
(2)在图(2)中画出一个三条边长分别为3,2$\sqrt{2}$,$\sqrt{5}$的三角形,使它的端点都在格点上.
分析 (1)根据长为4,宽为1的长方形的对角线长为$\sqrt{17}$进行作图即可;
(2)可先画3的线段,根据勾股定理可得长为$\sqrt{5}$的线段是长为2,宽为1的矩形的对角线,2$\sqrt{2}$是边长为2的正方形的对角线,据此作图即可;
解答 解:(1)如图1所示,线段AB即为所求;
(2)如图2所示,△CDE即为三条边长分别为3,2$\sqrt{2}$,$\sqrt{5}$的三角形.
点评 本题主要考查了无理数概念、勾股定理以及三角形有关知识的综合运用.解题时首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.一个等腰三角形的顶角是120°,则它的底角度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 不能确定 |
 如图,AC∥ED,AB∥FD,∠A=64°,则∠EDF的度数为64°.
如图,AC∥ED,AB∥FD,∠A=64°,则∠EDF的度数为64°.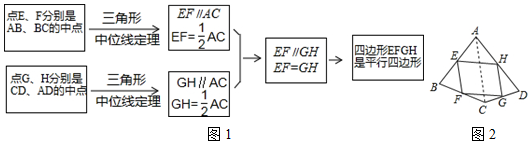
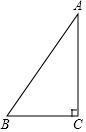 如图,在△ABC 中,∠C=90°
如图,在△ABC 中,∠C=90°