题目内容
6.先化简(1-$\frac{2}{x-1}$)•$\frac{{x}^{2}-x}{{x}^{2}-6x+9}$,再在1,2,3中选取一个适当的数代入求值.分析 此题只需先进行分式运算得到最简结果,再挑选出一个使分式有意义的值代入求得结果即可.
解答 解:(1-$\frac{2}{x-1}$)•$\frac{{x}^{2}-x}{{x}^{2}-6x+9}$,
=$\frac{x-1-2}{x-1}$•$\frac{x(x-1)}{(x-3)^{2}}$,
=$\frac{x}{x-3}$,
∵x-1≠0,x-3≠0,
∴x≠1,x≠3,
∴把x=2代入得:原式=$\frac{2}{2-3}$=-2.
点评 本题考查了分式的化简求值.注意:取适当的数代入求值时,要特别注意原式及化简过程中的每一步都有意义.

练习册系列答案
相关题目
16.下列说法中不正确的是( )
| A. | 选举中,人们通常最关心的数据是众数 | |
| B. | 从1,2,3,4,5中随机抽取一个数,取得奇数的可能性比较大 | |
| C. | 数据甲、乙的方差分别为S甲2=0.4,S乙2=0.6,则数据甲的波动小 | |
| D. | 数据3,5,4,1,-2的中位数是4 |
 如图,AC∥FG,∠1=∠2.请问AC与DE平行吗?为什么?
如图,AC∥FG,∠1=∠2.请问AC与DE平行吗?为什么?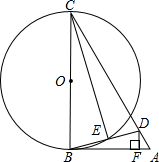 如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.
如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.
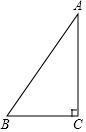 如图,在△ABC 中,∠C=90°
如图,在△ABC 中,∠C=90°