题目内容
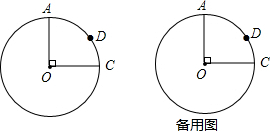
1. 如图,矩形的两条对角线夹角为60°,一条短边为3,则矩形的长边长为3$\sqrt{3}$.
如图,矩形的两条对角线夹角为60°,一条短边为3,则矩形的长边长为3$\sqrt{3}$.
分析 由矩形的性质和已知条件得出△AOB是等边三角形,得出OA=AB=3,AC=2OA=6,进而得出BC的长.
解答 解:∵四边形ABCD是矩形,
∴∠ABC=90°,OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=AB=3,
∴AC=2OA=6,
BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
则矩形的长边长为3$\sqrt{3}$;
故答案为:3$\sqrt{3}$.
点评 本题考查了矩形的性质、等边三角形的判定与性质、勾股定理;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,半圆O2,半圆O3,…,组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第101秒时,点P的坐标是(101,1).
如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,半圆O2,半圆O3,…,组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第101秒时,点P的坐标是(101,1). 如图,AC∥ED,AB∥FD,∠A=64°,则∠EDF的度数为64°.
如图,AC∥ED,AB∥FD,∠A=64°,则∠EDF的度数为64°.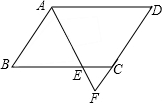 如图,在?ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,已知AB=6,AD=9,∠F=64°,求FC的长和∠B的度数.
如图,在?ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,已知AB=6,AD=9,∠F=64°,求FC的长和∠B的度数.