题目内容
7. 请在方格内画△ABC,使它的顶点都在格点上,且三边长分别为$\sqrt{2}$,$\sqrt{10}$,4$\sqrt{\frac{1}{2}}$.
请在方格内画△ABC,使它的顶点都在格点上,且三边长分别为$\sqrt{2}$,$\sqrt{10}$,4$\sqrt{\frac{1}{2}}$.(1)求△ABC的面积;
(2)求出最长边上的高;
(3)若点D与A,B,C三点是平行四边形的4个顶点,请在方格内画出所有符合条件的点D.
分析 (1)根据勾股定理逆定理判断三角形为直角三角形,再依据面积公式求解可得;
(2)设斜边上的高为h,根据(1)中所求面积列方程求解可得;
(3)根据平行四边形的判定,分别以直角三角形的三边为对角线作出点D即可得.
解答 解:(1)4$\sqrt{\frac{1}{2}}$=2$\sqrt{2}$,
∵($\sqrt{2}$)2+(2$\sqrt{2}$)2=($\sqrt{10}$)2,
∴△ABC是直角三角形,
∴S△ABC=$\frac{1}{2}$×$\sqrt{2}$×2$\sqrt{2}$=2;
(2)设最长边上的高为h,
则$\frac{1}{2}$×$\sqrt{10}$•h=2,
解得:h=$\frac{2\sqrt{10}}{5}$,
即最长边上的高为$\frac{2\sqrt{10}}{5}$;
(3)如图,点D1、D2、D3即为所求.
点评 本题主要考查勾股定理逆定理、三角形的面积公式及平行四边形的判定,熟练掌握平行四边形的判定是解题的关键.

练习册系列答案
相关题目
8.如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径总长度为( )


| A. | $\frac{16\sqrt{3}π}{3}$ | B. | $\frac{16π}{3}$ | C. | $\frac{4π}{3}+\frac{4\sqrt{3}π}{3}$ | D. | $\frac{8π}{3}+\frac{8\sqrt{3}π}{3}$ |
18.一个等腰三角形的顶角是120°,则它的底角度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 不能确定 |
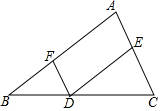 完成下面的证明.
完成下面的证明. 如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,半圆O2,半圆O3,…,组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第101秒时,点P的坐标是(101,1).
如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,半圆O2,半圆O3,…,组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第101秒时,点P的坐标是(101,1).