题目内容
12．因式分解：（1）x（a-b）2+y（b-a）2
（2）4x2-9．
分析 （1）提取公因式（a-b）2即可得；
（2）用平方差公式分解可得．
解答 解：（1）原式=x（a-b）2+y（a-b）2
=（x+y）（a-b）2；
（2）原式=（2x+3）（2x-3）．
点评 本题主要考查用提公因式法和公式法进行因式分解等基础知识，熟练掌握公式是解题的关键．
练习册系列答案
相关题目
17．
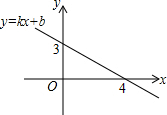已知一次函数y=kx+b（k、b为常数）的图象如图所示，那么关于x的不等式kx+b＞0的解集是（ ）
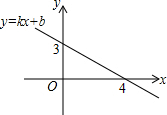已知一次函数y=kx+b（k、b为常数）的图象如图所示，那么关于x的不等式kx+b＞0的解集是（ ）| A． | x＞3 | B． | x＞4 | C． | x＜3 | D． | x＜4 |
3．已知$\frac{3x-3}{（x+1）（x-2）}$=$\frac{A}{x+1}$+$\frac{B}{x-2}$，则实数A，B分别为（ ）
| A． | 2，-1 | B． | -2，1 | C． | -2，-1 | D． | 2，1 |
4．下列分解因式正确的是（ ）
| A． | x2-x-2=（x-1）（x+2） | B． | -a2+a-$\frac{1}{4}$=$-\frac{1}{4}（2a-1）^{2}$ | ||
| C． | a（x-y）-b（y-x）=（x-y）（a-b） | D． | x2-4+2x=（x+2）（x-2）+2x |
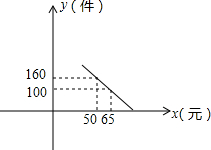某校两大学生积极响应“自主创业”的号召，准备利用一个月假期投资销售一种进价为每件40元的小家电，通过试管营销发现，当销售单价在40元至100元之间（含40元和100元）时，每月的销售量y（件）与销售单价x（元）之间的关系可近似地看作一次函数．其图象如图所示．