题目内容
1．分解因式（1）x2（a-b）-y2（a-b）
（2）9（a+b）2-4（a-b）2．
分析 （1）先提公因式a-b，再套用平方差公式分解；
（2）先用平方差公式分解，再化简即可．
解答 解：（1）原式=（a-b）（x2-y2）
=（a-b）（x+y）（x-y）；
（2）原式=[3（a+b）+2（a-b）][3（a+b）-2（a-b）]
=（5a+b）（a+5b）．
点评 本题考查了提公因式法，公式法分解因式．注意提取公因式后利用平方差公式进行二次分解，分解要彻底．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
6．解方程$\frac{x-1}{x}$-$\frac{2x}{x-1}$=3时，设$\frac{x-1}{x}$=y，则原方程可化为关于y的整式方程是（ ）
| A． | y-$\frac{2}{y}$=3 | B． | y2-2y=3 | C． | y2-3y-2=0 | D． | y2+3y-2=0 |
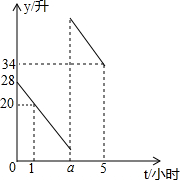张师傅驾车从甲地去乙地，途中在加油站加了一次油，加油时，车载电脑显示还能行驶50千米．假设加油前、后汽车都以100千米/小时的速度匀速行驶，已知油箱中剩余油量y（升）与行驶时间t（小时）之间的关系如图所示．
小东从甲地出发匀速前往相距20km的乙地，一段时间后，小明从乙地出发沿同一条路匀速前往甲地．小东出发2.5h后，在距乙地7.5km处与小明相遇，之后两人同时到达终点．图中线段AB、CD分别表示小东、小明与乙地的距离y（km）与小东所用时间x（h）的关系．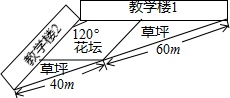
学校两幢教学楼之间有一块三角形地带，将其划分为三个区域：一块菱形和两块三角形．菱形作为花坛，两个三角形内铺上草皮，两幢教学楼的夹角为120°，其余尺寸如图所示，则菱形花坛的面积为$\frac{7200\sqrt{3}}{19}$m2．
