题目内容
17.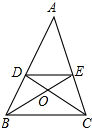 如图,已知DE∥BC,CD和BE相交于点O,S△DOE:S△COB=4:9,则AE:EC为( )
如图,已知DE∥BC,CD和BE相交于点O,S△DOE:S△COB=4:9,则AE:EC为( )| A. | 2:1 | B. | 2:3 | C. | 4:9 | D. | 5:4 |
分析 由DE∥BC,得到△DOE∽△COB,根据相似三角形的性质得到S△DOE:S△COB=($\frac{DE}{BC}$)2=4:9,求得$\frac{DE}{BC}$=$\frac{2}{3}$,通过△ADE∽△ABC,得到$\frac{AE}{AC}=\frac{DE}{BC}$=$\frac{2}{3}$,根据相似三角形的性质即可得到结论.
解答 解:∵DE∥BC,
∴△DOE∽△COB,
∴S△DOE:S△COB=($\frac{DE}{BC}$)2=4:9,
∴$\frac{DE}{BC}$=$\frac{2}{3}$,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AE}{AC}=\frac{DE}{BC}$=$\frac{2}{3}$,
∴AE:EC=2:1,
故选A.
点评 本题考查了相似三角形的判定和性质,证得$\frac{DE}{BC}$=$\frac{2}{3}$是解题的关键.

练习册系列答案
相关题目
5.下列各题的两个单项式为同类项的是( )
| A. | -$\frac{1}{2}$x2y与xy2 | B. | 3x2y与-4x2yz | C. | -3xy3与zy3 | D. | x2y与-3yx2 |
2.已知线段AB=3cm,反向延长线段AB到C,使BC=$\frac{5}{3}$AC,D是BC的中点,则线段AD的长为( )
| A. | $\frac{5}{2}$cm | B. | $\frac{5}{4}$cm | C. | $\frac{3}{2}$cm | D. | $\frac{1}{4}$cm |
9.已知函数y=2(x-3)2-4(1≤x≤6)的最大值与最小值的和为( )
| A. | 18 | B. | 0 | C. | 10 | D. | 无法确定 |
 已知,如图,在四边形ABCD中,AB=AD,∠ABC=∠ADC,求证:AC平分∠BAD.
已知,如图,在四边形ABCD中,AB=AD,∠ABC=∠ADC,求证:AC平分∠BAD. 如图所示,已知△ABC两内角的平分线AO、BO相交于点O,若∠AOB=140°,求∠C的度数.
如图所示,已知△ABC两内角的平分线AO、BO相交于点O,若∠AOB=140°,求∠C的度数.