题目内容
12．
如图所示，已知△ABC两内角的平分线AO、BO相交于点O，若∠AOB=140°，求∠C的度数．
分析 根据角平分线的定义和三角形的内角和定理求出∠CAB+∠CBA的值，再利用三角形的内角和定理求出∠C的度数即可．
解答 解：∵AO、BO分别平分∠CAB、∠ABC，
∴∠CAB=2∠OAB，∠CBA=2∠OBA，
∵∠OAB+∠OBA=180°-∠AOB=40°，
∴∠CAB+∠CBA=2（∠OAB+∠OBA）=80°，
∴在△ABC中，∠C=180°-80°=100°．
点评 本题考查了三角形的内角和定理和角平分线的性质，同时考查了整体思想的应用；难度适中．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
如图，在△ABC中，AB=AC，∠1=∠2，求证：∠3=∠4．
如图是一个风筝的图案，它是轴对称图形，EF是对称轴．∠A=90°，∠AED=130°，∠C=45°，则∠BFC的度数为140°．
17．
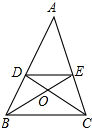如图，已知DE∥BC，CD和BE相交于点O，S△DOE：S△COB=4：9，则AE：EC为（ ）
如图，已知DE∥BC，CD和BE相交于点O，S△DOE：S△COB=4：9，则AE：EC为（ ）| A． | 2：1 | B． | 2：3 | C． | 4：9 | D． | 5：4 |
1．a是实数，则在下列说法中正确的一个是（ ）
| A． | -a是负数 | B． | a2是正数 | C． | -|a2|是负数 | D． | a2+0.001是正数 |