题目内容
9. 已知:如图,在菱形ABCD中,AE⊥BC于点E,且BE=CE,AD=2,求:
已知:如图,在菱形ABCD中,AE⊥BC于点E,且BE=CE,AD=2,求:(1)BD的长.
(2)菱形ABCD的面积.
分析 (1)利用菱形的性质结合等边三角形的判定与性质得出BO的长,即可得出BD的长;
(2)直接利用菱形对角线乘积的一半等于其面积,进而得出答案.
解答 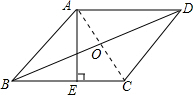 解:(1)连接AC,交BD于点O,
解:(1)连接AC,交BD于点O,
∵AE⊥BC于点E,且BE=CE,
∴AB=AC,
∵在菱形ABCD中,
∴AB=BC,
∴△ABC是等边三角形,
∴∠ABO=30°,
∵AD=2,
∴AB=2,BO=$\sqrt{3}$,
∴BD=2$\sqrt{3}$;
(2)菱形ABCD的面积为:$\frac{1}{2}$AC•BD=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$.
点评 此题主要考查了菱形的性质以及等边三角形的判定与性质,得出△ABC是等边三角形是解题关键.

练习册系列答案
相关题目
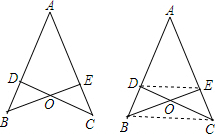 如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O. 如图,△BEF的面积比△ADF的面积少24cm2,△ABD的面积与△CDE的面积比是4:5,求平行四边形ABCD的面积.
如图,△BEF的面积比△ADF的面积少24cm2,△ABD的面积与△CDE的面积比是4:5,求平行四边形ABCD的面积.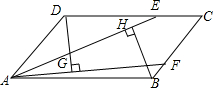 如图,点E,F分别在?ABCD的边DC,CB上,且AE=AF,DG⊥AF,BH⊥AE,垂足分别为G,H.求证:DG=BH.
如图,点E,F分别在?ABCD的边DC,CB上,且AE=AF,DG⊥AF,BH⊥AE,垂足分别为G,H.求证:DG=BH.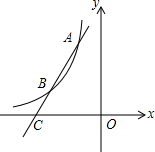 已知反比例函数y=$\frac{m-8}{x}$(m8≠8且m为常数)的图象经过点A(-1,6).
已知反比例函数y=$\frac{m-8}{x}$(m8≠8且m为常数)的图象经过点A(-1,6).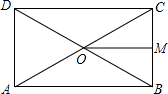 已知:如图,在?ABCD中,对角线AC,BD交于点O,OM⊥BC于点M,且BM=CM,求证:?ABCD是矩形.
已知:如图,在?ABCD中,对角线AC,BD交于点O,OM⊥BC于点M,且BM=CM,求证:?ABCD是矩形. 如图,在矩形ABCD中,对角线AC,BD交于点O,DE平分∠ADC,交BC于点E,∠BDE=15°,求∠COD与∠COE的度数.
如图,在矩形ABCD中,对角线AC,BD交于点O,DE平分∠ADC,交BC于点E,∠BDE=15°,求∠COD与∠COE的度数.