题目内容
4. 如图,△BEF的面积比△ADF的面积少24cm2,△ABD的面积与△CDE的面积比是4:5,求平行四边形ABCD的面积.
如图,△BEF的面积比△ADF的面积少24cm2,△ABD的面积与△CDE的面积比是4:5,求平行四边形ABCD的面积.
分析 根据平行四边形的性质得出S△ABD=S△CDB,由△BEF的面积比△ADF的面积少24cm2,可知△BED的面积比△ABD的面积少24cm2,即S△CDB-S△BED=24cm2,又△ABD的面积与△CDE的面积比是4:5,即△CBD的面积与△CDE的面积比是4:5,可设S△CBD=4xcm2,则S△CDE=5xcm2,S△BED=xcm2,代入S△CDB-S△BED=24cm2,求出x的值进而求解即可.
解答  解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴S△ABD=S△CDB,
又∵S△ADF-S△BEF=24cm2,
∴S△ABD-S△BED=24cm2,
S△CDB-S△BED=24cm2,
∵S△ABD:S△CDE=4:5,
∴S△CBD:S△CDE=4:5,
设S△CBD=4xcm2,则S△CDE=5xcm2,S△BED=xcm2,
∵S△CDB-S△BED=24cm2,
∴4x-x=24,
∴x=8,
∴S△ABD=S△CDB=32cm2,
∴平行四边形ABCD的面积=32×2=64cm2.
点评 本题考查了平行四边形的性质,解题的关键是根据三角形面积之间的等量代换,求出S△CDB-S△BED=24cm2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 以等腰△ABC的腰AB为直径作半圆,设圆心为点O,半圆与另一腰交于点D,与底BC交于点E,取线段CD的中点F,连接EF.
以等腰△ABC的腰AB为直径作半圆,设圆心为点O,半圆与另一腰交于点D,与底BC交于点E,取线段CD的中点F,连接EF. 如图,AB=AC,CD⊥AB于D,BE⊥AC于E,求证:AD=AE.
如图,AB=AC,CD⊥AB于D,BE⊥AC于E,求证:AD=AE.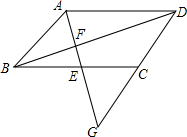 如图,直线AG过平行四边形ABCD的边BC的中点F、交对角线BD于点F,交DC的延长线于G.
如图,直线AG过平行四边形ABCD的边BC的中点F、交对角线BD于点F,交DC的延长线于G. 已知:如图,在菱形ABCD中,AE⊥BC于点E,且BE=CE,AD=2,求:
已知:如图,在菱形ABCD中,AE⊥BC于点E,且BE=CE,AD=2,求: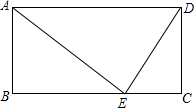 已知:如图,在矩形ABCD中,E为BC上一点.若AB=12,AD=25,BE=16,求证:△ABE∽△ECD.
已知:如图,在矩形ABCD中,E为BC上一点.若AB=12,AD=25,BE=16,求证:△ABE∽△ECD.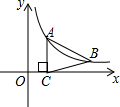 如图,点A、B在双曲线y=$\frac{k}{x}$(x>0)上,AC⊥x轴于C,且AB=BC,若S△ABC=6,求k的值.
如图,点A、B在双曲线y=$\frac{k}{x}$(x>0)上,AC⊥x轴于C,且AB=BC,若S△ABC=6,求k的值.