题目内容
1. 已知反比例函数y=$\frac{m-8}{x}$(m8≠8且m为常数)的图象经过点A(-1,6).
已知反比例函数y=$\frac{m-8}{x}$(m8≠8且m为常数)的图象经过点A(-1,6).(1)求m的值;
(2)求与反比例函数y=$\frac{m-8}{x}$(m≠8且m为常数)的图象仅有一个公共点A(-1,6)的直线的解析式;
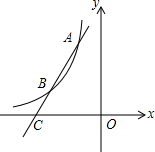
(3)如图所示,过点A作直线AC与函数y=$\frac{m-8}{x}$的图象相交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
分析 (1)将A点坐标代入反比例函数解析式即可得到一个关于m的一元一次方程,求出m的值;
(2)设直线解析式为为y=kx+b,把A(-1,6)求得b的值,得出y=kx+k+6,利用直线与反比例函数y=-$\frac{6}{x}$的图象仅有一个交点,由根的判别式求出k的值,即可求得直线的解析式.
(3)再分别过点A、B作x轴的垂线,垂足分别为点E、D,则△CBD∽△CAE,运用相似三角形知识求出CD的长即可求出点C的横坐标.
解答 解:(1)∵反比例函数y=$\frac{m-8}{x}$(m8≠8且m为常数)的图象经过点A(-1,6),
∴m-8=-1×6,
∴m=2.
(2)设与反比例函数y=$\frac{m-8}{x}$(m≠8且m为常数)的图象仅有一个公共点A(-1,6)的直线的解析式为y=kx+b,
把A(-1,6)代入得,6=-kx+b,
∴b=k+6,
∴y=kx+k+6,
代入y=-$\frac{6}{x}$得,-$\frac{6}{x}$=kx+k+6,
整理得kx2+(k+6)x+6=0,
根据题意△=(k+6)2-4k×6=0,
解得k=6,
∴直线的解析式为y=6x+12;
(3)如图,分别过点A、B作x轴的垂线,垂足分别为点E、D,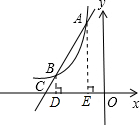
由题意得,AE=6,OE=1,
∵BD⊥x轴,AE⊥x轴,
∴AE∥BD,
∴△CBD∽△CAE,
∴$\frac{CB}{CA}$=$\frac{BD}{AE}$,
∵AB=2BC,
∴$\frac{CB}{CA}$=$\frac{1}{3}$,
∴$\frac{1}{3}$=$\frac{BD}{6}$,
∴BD=2.
即点B的纵坐标为2.
∵B在反比例函数y=-$\frac{6}{x}$的图象上,
∴2=-$\frac{6}{x}$,
∴x=-3,
∵点A(-1,6),点B(-3,2)
∴直线AB的解析式为:y=2x+8,
∴C(-4,0).
点评 本题考查了一次函数和反比例函数的交点问题,待定系数法求解析式,三角形相似的判定和性质,根据直线与反比例函数的图象仅有一个交点,由根的判别式求出是解题关键.

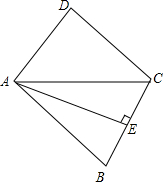 如图所示,在菱形ABCD中,AE⊥BC,E为垂足,且BE=CE,AB=2,求:
如图所示,在菱形ABCD中,AE⊥BC,E为垂足,且BE=CE,AB=2,求: 如图,AB=AC,CD⊥AB于D,BE⊥AC于E,求证:AD=AE.
如图,AB=AC,CD⊥AB于D,BE⊥AC于E,求证:AD=AE. 已知:如图,在菱形ABCD中,AE⊥BC于点E,且BE=CE,AD=2,求:
已知:如图,在菱形ABCD中,AE⊥BC于点E,且BE=CE,AD=2,求: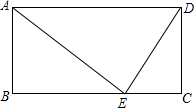 已知:如图,在矩形ABCD中,E为BC上一点.若AB=12,AD=25,BE=16,求证:△ABE∽△ECD.
已知:如图,在矩形ABCD中,E为BC上一点.若AB=12,AD=25,BE=16,求证:△ABE∽△ECD.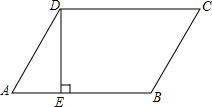 如图,在平行四边形ABCD中,AD=BC,AB=CD,DE⊥AB于点E,∠A=60°,BE=2AE=$\sqrt{72}$cm,求平行四边形ABCD的周长.
如图,在平行四边形ABCD中,AD=BC,AB=CD,DE⊥AB于点E,∠A=60°,BE=2AE=$\sqrt{72}$cm,求平行四边形ABCD的周长.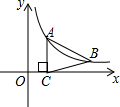 如图,点A、B在双曲线y=$\frac{k}{x}$(x>0)上,AC⊥x轴于C,且AB=BC,若S△ABC=6,求k的值.
如图,点A、B在双曲线y=$\frac{k}{x}$(x>0)上,AC⊥x轴于C,且AB=BC,若S△ABC=6,求k的值. 将一个宽度相等的纸条如图所示折叠一下,那么∠2=50°,∠1=65°.
将一个宽度相等的纸条如图所示折叠一下,那么∠2=50°,∠1=65°.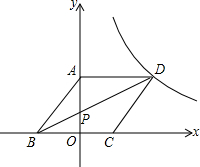 如图,边长为a的菱形ABCD的顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,A、C两点的坐标分别为(0,4)和(2,0).
如图,边长为a的菱形ABCD的顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,A、C两点的坐标分别为(0,4)和(2,0).