题目内容
2.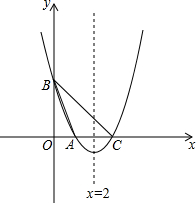 如图,抛物线y=x2-bx+c与x轴交于A、C两点,与y轴交于B点,已知A点坐标为(1,0),抛物线的对称轴为直线x=2.
如图,抛物线y=x2-bx+c与x轴交于A、C两点,与y轴交于B点,已知A点坐标为(1,0),抛物线的对称轴为直线x=2.(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)若点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出P点的坐标;若不存在,请说明理由.
分析 (1)根据A和C关于x=2对称即可求得C的坐标,然后把A和C的坐标代入抛物线解析式求得b和C的值,得到抛物线解析式;
(2)首先求得AC的长,然后利用三角形面价公式求解;
(3)直线BC与对称轴x=2的交点就是P,首先利用待定系数法求得BC的解析式,进而求得P的坐标.
解答 解:(1)A(1,0)关于x=2的对称点是(3,0),则C的坐标是(3,0).
根据题意得:$\left\{\begin{array}{l}{1-b+c=0}\\{9-3b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=4}\\{c=3}\end{array}\right.$,
则抛物线的解析式是y=x2-4x+3;
(2)AC=3-1=2,
则S△ABC=$\frac{1}{2}$AC•OB=$\frac{1}{2}$×2×3=3;
(3)C是A关于对称轴的对称点,则BC与对称轴的交点就是P.
设BC的解析式是y=kx+d,
则$\left\{\begin{array}{l}{d=3}\\{3k+d=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{d=3}\\{k=-1}\end{array}\right.$,
则直线BC的解析式是y=-x+3.
当x=2时,y=-2+3=1,
则P的坐标是(2,1).
点评 本题考查了待定系数法求函数解析式,正确理解P的位置是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.x的4倍与7的差不小于-1,可列关系式为( )
| A. | 4x-7≤-1 | B. | 4x-7<-1 | C. | 4x-7=-1 | D. | 4x-7≥-1 |
 如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,求⊙O的半径.
如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,求⊙O的半径. 已知二次函数y1=x2+2x+m-5.
已知二次函数y1=x2+2x+m-5. 如图,将一张纸条折叠,若∠1=54°,则∠2的度数为72°.
如图,将一张纸条折叠,若∠1=54°,则∠2的度数为72°. 已知线段AB=42,点C是线段AB的中点,点D是线段CB的中点,点E在线段AB上,且CE=$\frac{1}{3}$AC,求线段DE的长.
已知线段AB=42,点C是线段AB的中点,点D是线段CB的中点,点E在线段AB上,且CE=$\frac{1}{3}$AC,求线段DE的长.