题目内容
18.阅读下面的材料:小明遇到一个问题:如图1,在?ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.如果$\frac{AF}{EF}$=3,求$\frac{CD}{CG}$的值.他的做法是:过点E作EH∥AB交BG于点H,那么可以得到△BAF∽△HEF.请回答:
(1)AB和EH之间的数量关系是AB=3EH,CG和EH之间的数量关系是CG=2EH,$\frac{CD}{CG}$的值为$\frac{3}{2}$.
(2)参考小明思考问题的方法,解决问题:
如图2,在四边形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F.如果$\frac{AB}{CD}$=2,$\frac{BC}{BE}=\frac{2}{3}$,求$\frac{AF}{EF}$的值.
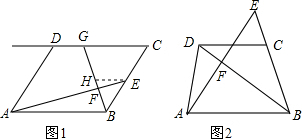
分析 (1)先根据EH∥AB,$\frac{AF}{EF}$=3得出AB=3EH,再根据四边形ABCD是平行四边形,点E是边BC的中点得出CG=2EH=2x,再求出$\frac{CD}{CG}$=$\frac{3}{2}$即可;
(2)过点E作EH∥AB交BD的延长线于点H,根据EH∥CD,得出CD=$\frac{2}{3}$EH,根据AB=2CD=$\frac{4}{3}$EH,得出$\frac{AB}{EH}$=$\frac{4}{3}$,最后根据EH∥AB得出$\frac{AF}{EF}$=$\frac{AB}{EH}$即可求出答案.
解答 解:(1)如图1,
∵EH∥AB,
∴$\frac{AF}{EF}$=$\frac{AB}{EH}$=3,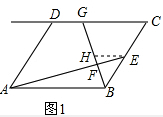
∴AB=3EH,
设EH=x,则AB=3x,
∵四边形ABCD是平行四边形,
∴CD=AB=3x,AB∥CD,
∴HE∥CD,
∵点E是边BC的中点,
∴CG=2EH=2x,
∴$\frac{CD}{CG}$=$\frac{3x}{2x}$=$\frac{3}{2}$,
故答案为:AB=3EH,CG=2EH,$\frac{3}{2}$;
(2)如图2,过点E作EH∥AB交BD的延长线于点H.
∵AB∥CD,
∴EH∥CD,
∴$\frac{CD}{EH}=\frac{BC}{BE}=\frac{2}{3}$,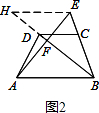
∴CD=$\frac{2}{3}$EH,
∵$\frac{AB}{CD}$=2,
∴AB=2CD=$\frac{4}{3}$EH,
∴$\frac{AB}{EH}$=$\frac{4}{3}$,
∵EH∥AB,
∴△ABF∽△EHF.
∴$\frac{AF}{EF}$=$\frac{AB}{EH}$=$\frac{4}{3}$.
点评 此题考查了相似形综合,用到的知识点是相似三角形的判定与性质、平行四边形的性质,关键是根据题意作出辅助线,构造相似三角形,注意知识的综合运用和比例式的变形.

 一课一练课时达标系列答案
一课一练课时达标系列答案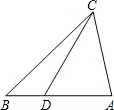 如图,要使△ACD∽△ABC,需要补充的一个条件是( )
如图,要使△ACD∽△ABC,需要补充的一个条件是( )| A. | $\frac{AC}{CD}$=$\frac{BA}{BC}$ | B. | $\frac{CD}{AD}$=$\frac{BC}{AC}$ | C. | CD2=AD•DB | D. | AC2=AD•AB |
| A. | 没有实根 | B. | 有两个相等的实根 | ||
| C. | 有两个不等的实根 | D. | 有两个实根 |
| A. | b3•b3=b9 | B. | (-x3y)•(xy2)=x4y3 | C. | (-2x3)2=-4x6 | D. | (-a2)3=-a6 |
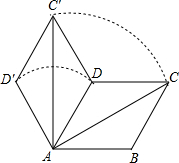 如图,菱形ABCD的边长为4,∠BAD=60°,AC为对角线.将△ACD绕点A逆时针旋转60°得到△AC′D′,连结DC′.
如图,菱形ABCD的边长为4,∠BAD=60°,AC为对角线.将△ACD绕点A逆时针旋转60°得到△AC′D′,连结DC′.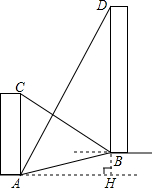 如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是1:2$\sqrt{3}$,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)
如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是1:2$\sqrt{3}$,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)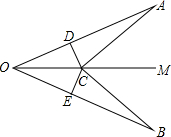 已知:如图,OM是∠AOB的平分线,C是OM上一点,且CD⊥OA于D,CE⊥OB于E,AD=EB.求证:AC=CB.
已知:如图,OM是∠AOB的平分线,C是OM上一点,且CD⊥OA于D,CE⊥OB于E,AD=EB.求证:AC=CB.