题目内容
9.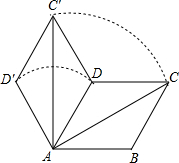 如图,菱形ABCD的边长为4,∠BAD=60°,AC为对角线.将△ACD绕点A逆时针旋转60°得到△AC′D′,连结DC′.
如图,菱形ABCD的边长为4,∠BAD=60°,AC为对角线.将△ACD绕点A逆时针旋转60°得到△AC′D′,连结DC′.(1)求证:△ADC≌△ADC′.
(2)求在旋转过程中线段CD扫过图形的面积.(结果保留π).
分析 (1)如图,首先运用旋转变换的性质证明AC=AC′,∠CAD=∠C′AD,进而运用SAS公理证明△CAD≌△C′AD;
(2)如图,作辅助线,求出线段AC的长度,此为解决问题的关键性结论;判断出λ=S扇形CAC′S扇形DAD′,此为解决问题的另一关键性结论,运用扇形的面积公式即可解决问题.
解答  解:(1)如图,由题意得:AC=AC′,∠CAC′=60°,
解:(1)如图,由题意得:AC=AC′,∠CAC′=60°,
∵∠BAD=60°,
∴∠BAD=∠CAC′,
∴∠CAD=∠CAB=∠C′AD;
在△CAD与△C′AD中,
$\left\{\begin{array}{l}{CA=C′A}\\{∠CAD=∠C′AD}\\{AD=AD}\end{array}\right.$,
∴△CAD≌△C′AD(SAS).
(2)如图,连接BD,交AC于点E;
设在旋转过程中线段CD扫过图形的面积为λ;
∵四边形ABCD为菱形,且∠DAB=60°,
∴∠DAE=30°,DE⊥AE,AE=CE;
∴AE=AD•cos30°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴AC=2AE=4$\sqrt{3}$;
∵△CAD≌△C′AD,
∴λ=S扇形CAC′-S扇形DAD′
=$\frac{60π×(4\sqrt{3})^{2}}{360}-\frac{60π×{4}^{2}}{360}$
=$\frac{16}{3}π$.
点评 该题以菱形为载体,在考查菱形性质的同时,还考查了全等三角形的判定、扇形的面积公式等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用全等三角形的判定、扇形的面积公式等几何知识点来分析、判断、推理或解答.

练习册系列答案
相关题目
19.已知∠α的补角为54°,∠β的余角为48°,则∠α的度数比∠β的度数多( )
| A. | 84° | B. | 74° | C. | 48° | D. | 60° |
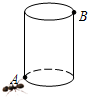 如图,有一个底边半径为6cm,高为24cm的圆柱,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与A点相对的B处的食物,试问:它需要爬行的最短路程越是多少?
如图,有一个底边半径为6cm,高为24cm的圆柱,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与A点相对的B处的食物,试问:它需要爬行的最短路程越是多少? 如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,求坡面AB的长.
如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,求坡面AB的长.