题目内容
8.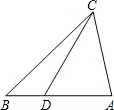 如图,要使△ACD∽△ABC,需要补充的一个条件是( )
如图,要使△ACD∽△ABC,需要补充的一个条件是( )| A. | $\frac{AC}{CD}$=$\frac{BA}{BC}$ | B. | $\frac{CD}{AD}$=$\frac{BC}{AC}$ | C. | CD2=AD•DB | D. | AC2=AD•AB |
分析 由于两三角形有公共角,若根据有两组角对应相等的两个三角形相似添加条件,则∠ACD=∠B;若根据两组对应边的比相等且夹角对应相等的两个三角形相似添加条件,则$\frac{AC}{AB}$=$\frac{AD}{AC}$,然后对各选项进行判断.
解答 解:∵∠CAD=∠BAC,
∴当∠ACD=∠B时,△ACD∽△ABC;
当$\frac{AC}{AB}$=$\frac{AD}{AC}$,即AC2=AD•AB时,△ACD∽△ABC.
故选D.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.

练习册系列答案
相关题目
18.在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c三边,则下列式子一定成立的是( )
| A. | a=c•sinB | B. | a=c•cosB | C. | $c=\frac{a}{tanB}$ | D. | c=a•sinA |
19.已知∠α的补角为54°,∠β的余角为48°,则∠α的度数比∠β的度数多( )
| A. | 84° | B. | 74° | C. | 48° | D. | 60° |
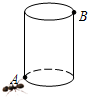 如图,有一个底边半径为6cm,高为24cm的圆柱,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与A点相对的B处的食物,试问:它需要爬行的最短路程越是多少?
如图,有一个底边半径为6cm,高为24cm的圆柱,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与A点相对的B处的食物,试问:它需要爬行的最短路程越是多少?