题目内容
3.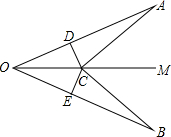 已知:如图,OM是∠AOB的平分线,C是OM上一点,且CD⊥OA于D,CE⊥OB于E,AD=EB.求证:AC=CB.
已知:如图,OM是∠AOB的平分线,C是OM上一点,且CD⊥OA于D,CE⊥OB于E,AD=EB.求证:AC=CB.
分析 先由角平分线的性质得出CD=CE,再由SAS证明△ADC≌△BEC,得出对应边相等即可.
解答 证明:∵OM是∠AOB的平分线,C是OM上一点,
且CD⊥OA于D,CE⊥OB于E,
∴CD=CE,∠ADC=∠BEC=90°,
在△ACD和△BCE中,
$\left\{\begin{array}{l}AD=EB\\∠ADC=∠BEC\\ DC=CE\end{array}\right.$,
∴△ADC≌△BEC(SAS),
∴AC=CB.
点评 本题考查了全等三角形的判定与性质、角平分线的性质;证明三角形全等得出对应边相等是解决问题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
11.下列是三元一次方程组$\left\{\begin{array}{l}{x+2y+z=16}\\{2x=3y=6z}\end{array}\right.$的解的是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=3}\\{z=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=6}\\{y=3}\\{z=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=6}\\{y=4}\\{z=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=5}\\{z=6}\end{array}\right.$ |
8.中新网2014年11月19日电 据财政部网站消息,为保证城乡义务教育阶段学校春季开学后正常运转和“两免一补”政策落实到位,中央财政下达2015年城乡义务教育补助经费部分预算697.2亿元.将697.2亿用科学记数法表示应为( )
| A. | 6.972×1011 | B. | 6.972×1010 | C. | 0.6972×103 | D. | 6.972×102 |
15.将点A(-1,2)沿x轴向右平移3个单位长度,再沿y轴向下平移4个单位长度后得到点A′的坐标为( )
| A. | (-4,-2 ) | B. | (2,-2 ) | C. | (-4,6 ) | D. | (2,6 ) |
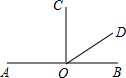 如图,已知OC⊥AB,如果∠BOD=30°,则∠COD的度数为60°.
如图,已知OC⊥AB,如果∠BOD=30°,则∠COD的度数为60°.