题目内容
11.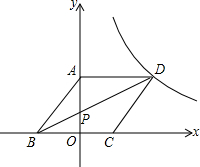 如图,边长为a的菱形ABCD的顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,A、C两点的坐标分别为(0,4)和(2,0).
如图,边长为a的菱形ABCD的顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,A、C两点的坐标分别为(0,4)和(2,0).(1)求反比例函数的解析式;
(2)连接BD,交y轴于点P,求tan∠DBC的值和OP的长.
分析 (1)由四边形ABCD是菱形,可求得BC=AD=a,又由A、C两点的坐标分别为(0,4)和(2,0),可得OB=a-2,OA=4,然后由在Rt△ABO中,OB2+OA2=AB2,求得a的值,继而求得点D的坐标,即可求得答案;
(2)首先过点E作DE⊥x轴于点E,即可求得DE与BE的长,继而求得答案.
解答 解:(1)∵四边形ABCD是菱形,
∴BC=AD=a,
∵A、C两点的坐标分别为(0,4)和(2,0),
∴OB=a-2,OA=4,
在Rt△ABO中,OB2+OA2=AB2,
∴(a-2)2+42=a2,
解得:a=5,
∴AD=5,
∴点D的坐标为:(5,4),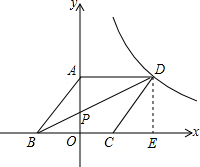 ∴k=xy=5×4=20,
∴k=xy=5×4=20,
∴反比例函数的解析式为:y=$\frac{20}{x}$;
(2)过点E作DE⊥x轴于点E,
则DE=4,OE=5,OB=a-2=3,
∴BE=OB+OE=5-2+5=8,
在Rt△DBE中,tan∠DBC=$\frac{DE}{BE}$=$\frac{4}{8}$=$\frac{1}{2}$;
在Rt△BOP中,OP=OB•tan∠DBC=3×$\frac{1}{2}$=$\frac{3}{2}$.
点评 此题考查了菱形的性质、反比例函数的性质、勾股定理以及三角函数等知识.注意求得a的值是解此题的关键.

练习册系列答案
相关题目
 已知反比例函数y=$\frac{m-8}{x}$(m8≠8且m为常数)的图象经过点A(-1,6).
已知反比例函数y=$\frac{m-8}{x}$(m8≠8且m为常数)的图象经过点A(-1,6).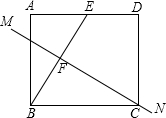 如图,长方形纸片ABCD中,CD=4,点E是AD上的-点,且AE=2,BE的垂直平分线MN恰好过点C,求矩形的一边AD的长度.
如图,长方形纸片ABCD中,CD=4,点E是AD上的-点,且AE=2,BE的垂直平分线MN恰好过点C,求矩形的一边AD的长度. 如图,在矩形ABCD中,对角线AC,BD交于点O,DE平分∠ADC,交BC于点E,∠BDE=15°,求∠COD与∠COE的度数.
如图,在矩形ABCD中,对角线AC,BD交于点O,DE平分∠ADC,交BC于点E,∠BDE=15°,求∠COD与∠COE的度数.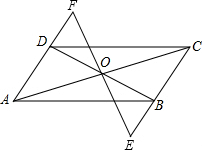 如图,在?ABCD中,对角线AC,BD交于点O,过点O的直线分别交CB,AD的延长线于点E,F,BE与DF相等吗?为什么?
如图,在?ABCD中,对角线AC,BD交于点O,过点O的直线分别交CB,AD的延长线于点E,F,BE与DF相等吗?为什么?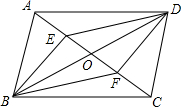 如图,已知四边形ABCD、EBFD均为平行四边形,AC、BD相交于点O,且A、E、O、F、C在同一条直线上,AC=8cm,AE=2cm,试求EF的长.
如图,已知四边形ABCD、EBFD均为平行四边形,AC、BD相交于点O,且A、E、O、F、C在同一条直线上,AC=8cm,AE=2cm,试求EF的长.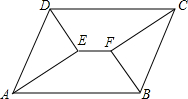 如图,?ABCD中,AB>AD,∠A与∠D的平分线交于点E,∠B与∠C的平分线交于点F,连接EF.请证明:EF=AB-BC.
如图,?ABCD中,AB>AD,∠A与∠D的平分线交于点E,∠B与∠C的平分线交于点F,连接EF.请证明:EF=AB-BC. 已知矩形ABCD的两条对角线相交于O,∠AOD=120°,AD=3cm,求:
已知矩形ABCD的两条对角线相交于O,∠AOD=120°,AD=3cm,求: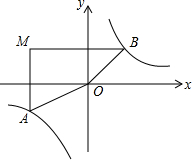 如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=$\frac{2}{x}$的图象交于A、B两点,则四边形MAOB的面积为8.
如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=$\frac{2}{x}$的图象交于A、B两点,则四边形MAOB的面积为8.