题目内容
16.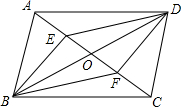 如图,已知四边形ABCD、EBFD均为平行四边形,AC、BD相交于点O,且A、E、O、F、C在同一条直线上,AC=8cm,AE=2cm,试求EF的长.
如图,已知四边形ABCD、EBFD均为平行四边形,AC、BD相交于点O,且A、E、O、F、C在同一条直线上,AC=8cm,AE=2cm,试求EF的长.
分析 根据平行四边形的性质得到AD=BC.AD∥BC,DE=BF,DE∥BF,由平行线的性质得到∠ADO=∠CBO,∠EDO=∠FBO,根据角的和差得到∠ADE=∠CBF,推出△ADE≌△CBF,由全等三角形的性质得到AE=CF=2cm,于是得到结论.
解答 解:∵四边形ABCD、EBFD均为平行四边形,
∴AD=BC.AD∥BC,DE=BF,DE∥BF,
∴∠ADO=∠CBO,∠EDO=∠FBO,
∴∠ADE=∠CBF,
在△ADE与△CBF中,$\left\{\begin{array}{l}{AD=CB}\\{∠ADE=∠CBF}\\{DE=BF}\end{array}\right.$,
∴△ADE≌△CBF,
∴AE=CF=2cm,
∵AC=8cm,
∴EF=AC-AE-CF=4cm.
点评 本题考查了平行线的性质,全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.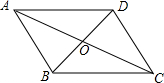 如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )
如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )
 如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )
如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )| A. | DC=BC | B. | AC⊥BD | C. | AB=BD | D. | ∠ADB=∠CDB |
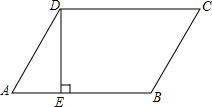 如图,在平行四边形ABCD中,AD=BC,AB=CD,DE⊥AB于点E,∠A=60°,BE=2AE=$\sqrt{72}$cm,求平行四边形ABCD的周长.
如图,在平行四边形ABCD中,AD=BC,AB=CD,DE⊥AB于点E,∠A=60°,BE=2AE=$\sqrt{72}$cm,求平行四边形ABCD的周长.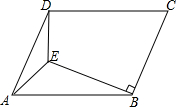 如图,E是?ABCD内一点,ED⊥CD,EB⊥BC,∠AED=135°,连CE交AD于F.
如图,E是?ABCD内一点,ED⊥CD,EB⊥BC,∠AED=135°,连CE交AD于F.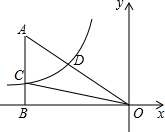 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-8,6),则△AOC的面积为18.
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-8,6),则△AOC的面积为18.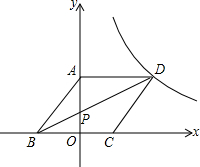 如图,边长为a的菱形ABCD的顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,A、C两点的坐标分别为(0,4)和(2,0).
如图,边长为a的菱形ABCD的顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,A、C两点的坐标分别为(0,4)和(2,0).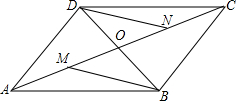 如图所示,?ABCD的对角线AC,BD相交于O,M是AO的中点,N是CO的中点,则BM与DN有什么关系?证明你的结论.
如图所示,?ABCD的对角线AC,BD相交于O,M是AO的中点,N是CO的中点,则BM与DN有什么关系?证明你的结论. 如图,在矩形ABCD中,对角线AC、BD相交于点O.求证:AC=BD.
如图,在矩形ABCD中,对角线AC、BD相交于点O.求证:AC=BD.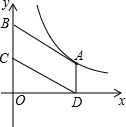 如图,在平面直角坐标系中,?ABCD的顶点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,顶点B、C在y轴正半轴上(点B在点C的上方),若点D的坐标为(3,0),?ABCD的面积为4.5,则k的值为4.5.
如图,在平面直角坐标系中,?ABCD的顶点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,顶点B、C在y轴正半轴上(点B在点C的上方),若点D的坐标为(3,0),?ABCD的面积为4.5,则k的值为4.5.