题目内容
3.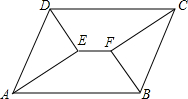 如图,?ABCD中,AB>AD,∠A与∠D的平分线交于点E,∠B与∠C的平分线交于点F,连接EF.请证明:EF=AB-BC.
如图,?ABCD中,AB>AD,∠A与∠D的平分线交于点E,∠B与∠C的平分线交于点F,连接EF.请证明:EF=AB-BC.
分析 易得∠AMD=∠ABF,故EM∥BF,由ASA证明△ADE≌△CBF,得出DE═BF.因此EM=BF,证出四边形EFBM是平行四边形,得出EF=BM,即可得出结论.
解答 证明:延长DE交AB于M,如图所示: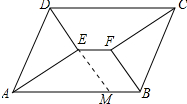
∵四边形ABCD是平行四边形,
∴AD=BC,CD∥AB,∠ADC=∠ABC,∴∠ADC+∠BAD=180°,∠CDM=∠AME,
∵AE、DE分别平分∠DAB和∠ADC
∴AE⊥DM,AE平分∠DAB.
∴ED=EM,∴AM=AD=BC,
∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,
∵BF平分∠ABC,CF平分∠BCD,
∴∠DAE=∠BCF,∠ADE=∠AMD=∠ABF=∠CBF,
∴EM∥BF,
在△ADE和△BCF中,$\left\{\begin{array}{l}{∠ADE=∠CBF}&{\;}\\{AD=CB}&{\;}\\{∠DAE=∠BCF}&{\;}\end{array}\right.$,
∴△ADE≌△CBF(ASA),
∴DE=BF.∴EM=BF,
∴四边形EFBM是平行四边形.
∴EF=MB,
∵BM=AB-AM=AB-BC,
∴EF=AB-BC.
点评 本题考查的是平行四边形的性质,要求学生在平行四边形中利用角平分线的性质或分解出线线间的关系并比较大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13. 如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
 如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )| A. | $\frac{AF}{AB}$=$\frac{AE}{DE}$ | B. | $\frac{AF}{CD}$=$\frac{AE}{BC}$ | C. | $\frac{AF}{AB}=\frac{EF}{CE}$ | D. | $\frac{DE}{AE}=\frac{CE}{EF}$ |
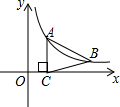 如图,点A、B在双曲线y=$\frac{k}{x}$(x>0)上,AC⊥x轴于C,且AB=BC,若S△ABC=6,求k的值.
如图,点A、B在双曲线y=$\frac{k}{x}$(x>0)上,AC⊥x轴于C,且AB=BC,若S△ABC=6,求k的值.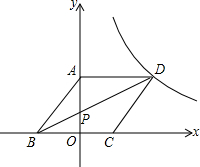 如图,边长为a的菱形ABCD的顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,A、C两点的坐标分别为(0,4)和(2,0).
如图,边长为a的菱形ABCD的顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,A、C两点的坐标分别为(0,4)和(2,0). 如图,在矩形ABCD中,对角线AC、BD相交于点O.求证:AC=BD.
如图,在矩形ABCD中,对角线AC、BD相交于点O.求证:AC=BD.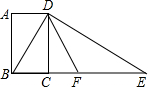 如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=3.设AB=x,AD=y,则x2+(y-3)2的值为9.
如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=3.设AB=x,AD=y,则x2+(y-3)2的值为9.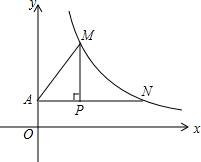 如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,交双曲线y=$\frac{k}{x}$(x>0)于点N;作PM⊥AN交双曲线y=$\frac{k}{x}$(x>0)于点M,连接AM.已知PN=4.
如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,交双曲线y=$\frac{k}{x}$(x>0)于点N;作PM⊥AN交双曲线y=$\frac{k}{x}$(x>0)于点M,连接AM.已知PN=4.