题目内容
2．
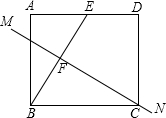如图，长方形纸片ABCD中，CD=4，点E是AD上的-点，且AE=2，BE的垂直平分线MN恰好过点C，求矩形的一边AD的长度．
分析 连接EC，先证明BC=EC=AD，设BC=EC=AD=x，在RT△CDE中利用勾股定理即可解决．
解答 解：如图连接
EC，
∵四边形ABCD是矩形，
∴AD=BC，AB=CD，∠D=90°，设BC=AD=x，
∵CF垂直平分BE，
∴BC=CE=x，
在RT△ABE中，∵∠D=90°，CD=4，ED=x-2，EC=x，
∴x2=（x-2）2+42，
∴x=5，
∴AD=5．
点评 本题考查矩形的性质、垂直平分线的性质、勾股定理等知识，解题的关键是利用勾股定理列出方程，学会转化的思想，属于中考常考题型．
练习册系列答案
相关题目
如图，AB=AC，CD⊥AB于D，BE⊥AC于E，求证：AD=AE．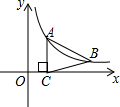
如图，点A、B在双曲线y=$\frac{k}{x}$（x＞0）上，AC⊥x轴于C，且AB=BC，若S△ABC=6，求k的值．
将一个宽度相等的纸条如图所示折叠一下，那么∠2=50°，∠1=65°．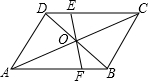
如图，O为?ABCD的对角线的交点，过O点作直线EF分别交CD，AB于点E，F．
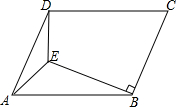如图，E是?ABCD内一点，ED⊥CD，EB⊥BC，∠AED=135°，连CE交AD于F．
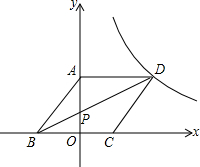如图，边长为a的菱形ABCD的顶点D在反比例函数y=$\frac{k}{x}$（x＞0）的图象上，A、C两点的坐标分别为（0，4）和（2，0）．
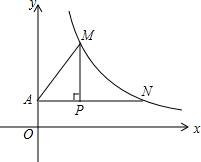如图，点P的坐标为（2，$\frac{3}{2}$），过点P作x轴的平行线交y轴于点A，交双曲线y=$\frac{k}{x}$（x＞0）于点N；作PM⊥AN交双曲线y=$\frac{k}{x}$（x＞0）于点M，连接AM．已知PN=4．