题目内容
按要求分别写出以x为未知数的一元二次方程:①两根分别为2+
,2-
: ;②二次项系数不为1,且两根互为倒数: ;③有一根为0: ;④有两个相等的实数根: ;⑤有一根为-1: ;⑥无实数根: .
| 5 |
| 5 |
考点:根与系数的关系,一元二次方程的解,根的判别式
专题:
分析:①设此一元二次方程为x2+px+q=0,由二次项系数为1,两根分别为2+
,2-
,根据根与系数的关系可得p=-(2+
+2-
)=-4,q=(2+
)(2-
)=-1,即可得到满足题意的一个方程;
②因为方程有两根,所以△≥0;由于两根互为倒数,所以两根之积等于1,即二次项系数等于常数项.只要满足上述条件的方程即为所求;
③设方程的两根是0和1,因而方程是x(x-1)=0即x2-x=0,本题答案不唯一;
④一元二次方程有两个相等的实数根,判别式等于0.答案不唯一;
⑤有一个根是-1的一元二次方程有无数个,只要含有因式x+1的一元二次方程都有一个根是-1;
⑥写出一个一元二次方程,然后确定根的判别式的值小于0即可.
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
②因为方程有两根,所以△≥0;由于两根互为倒数,所以两根之积等于1,即二次项系数等于常数项.只要满足上述条件的方程即为所求;
③设方程的两根是0和1,因而方程是x(x-1)=0即x2-x=0,本题答案不唯一;
④一元二次方程有两个相等的实数根,判别式等于0.答案不唯一;
⑤有一个根是-1的一元二次方程有无数个,只要含有因式x+1的一元二次方程都有一个根是-1;
⑥写出一个一元二次方程,然后确定根的判别式的值小于0即可.
解答:解:①设此一元二次方程为x2+px+q=0,
∵二次项系数为1,两根分别为2+
,2-
,
∴p=-(2+
+2-
)=-4,q=(2+
)(2-
)=-1,
∴这个方程为:x2+4x-1=0(答案不唯一);
(2)∵两根互为倒数,
∴两根之积等于1,即二次项系数等于常数项.
又∵方程有两根,
∴△≥0.
设方程为ax2+bx+a=0,且b2-4a2≥0.
∴满足条件的方程可写为2x2+5x+2=0(答案不唯一);
③设方程的另一根为1,
则根据因式分解法可得方程为x(x-1)=0,
即x2-x=0(答案不唯一);
④∵一元二次方程ax2+bx+c=0(a≠0)有两个相等的实数根,
∴b2-4ac=0,
符合条件的一元二次方程可以为x2+2x+1=0(答案不唯一);
⑤形如(x+1)(ax+b)=0(a≠0)的一元二次方程都有一个根是-1,
当a=1,b=0时,可以写出一个一元二次方程:x2+x=0(答案不唯一);
⑥对于方程x2-x+3=0,
∵△=12-4×1×3=-12<0,
∴x2-x+3=0无实数根.
∴符合条件的一元二次方程可以为x2-x+3=0(答案不唯一).
故答案为x2+4x-1=0;2x2+5x+2=0;x2-x=0;x2+2x+1=0;x2+x=0;x2-x+3=0.
∵二次项系数为1,两根分别为2+
| 5 |
| 5 |
∴p=-(2+
| 5 |
| 5 |
| 5 |
| 5 |
∴这个方程为:x2+4x-1=0(答案不唯一);
(2)∵两根互为倒数,
∴两根之积等于1,即二次项系数等于常数项.
又∵方程有两根,
∴△≥0.
设方程为ax2+bx+a=0,且b2-4a2≥0.
∴满足条件的方程可写为2x2+5x+2=0(答案不唯一);
③设方程的另一根为1,
则根据因式分解法可得方程为x(x-1)=0,
即x2-x=0(答案不唯一);
④∵一元二次方程ax2+bx+c=0(a≠0)有两个相等的实数根,
∴b2-4ac=0,
符合条件的一元二次方程可以为x2+2x+1=0(答案不唯一);
⑤形如(x+1)(ax+b)=0(a≠0)的一元二次方程都有一个根是-1,
当a=1,b=0时,可以写出一个一元二次方程:x2+x=0(答案不唯一);
⑥对于方程x2-x+3=0,
∵△=12-4×1×3=-12<0,
∴x2-x+3=0无实数根.
∴符合条件的一元二次方程可以为x2-x+3=0(答案不唯一).
故答案为x2+4x-1=0;2x2+5x+2=0;x2-x=0;x2+2x+1=0;x2+x=0;x2-x+3=0.
点评:此题考查了根的判别式,根与系数的关系,一元二次方程的根即方程的解的定义,用到的知识点:
一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac的关系为:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.上面的结论反过来也成立.
x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
,反过来也成立,即
=-(x1+x2),
=x1x2.
能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.
一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac的关系为:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.上面的结论反过来也成立.
x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
| b |
| a |
| c |
| a |
| b |
| a |
| c |
| a |
能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
利用数轴,可得式子|x-1|+|x-2|+|x-3|的最小值是( )
| A、1 | B、2 | C、0 | D、6 |
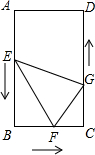 如图,在长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB=DC=12cm,BC=AD=8cm,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向运动.点F、G的速度为2m/s,点E的速度为4m/s,设移动开始后第ts时,△EFG的面积为S(cm2).
如图,在长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB=DC=12cm,BC=AD=8cm,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向运动.点F、G的速度为2m/s,点E的速度为4m/s,设移动开始后第ts时,△EFG的面积为S(cm2). 如图,等腰梯形ABCD中,AB=CD=5,点A到x轴的距离为4,点C的坐标为(9,0),则点D的坐标为
如图,等腰梯形ABCD中,AB=CD=5,点A到x轴的距离为4,点C的坐标为(9,0),则点D的坐标为 有A、B两个村长10km,做一条道,使A到这条道的距离为4km,B到这条道的距离是6km,有几种修法?
有A、B两个村长10km,做一条道,使A到这条道的距离为4km,B到这条道的距离是6km,有几种修法?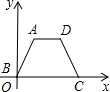 如图所示,梯形ABCD中,AB=DC=5,点A到x轴的距离是4,点C的坐标是(9,0),则梯形ABCD的面积是
如图所示,梯形ABCD中,AB=DC=5,点A到x轴的距离是4,点C的坐标是(9,0),则梯形ABCD的面积是