题目内容
 如图,等腰梯形ABCD中,AB=CD=5,点A到x轴的距离为4,点C的坐标为(9,0),则点D的坐标为
如图,等腰梯形ABCD中,AB=CD=5,点A到x轴的距离为4,点C的坐标为(9,0),则点D的坐标为考点:等腰梯形的性质,坐标与图形性质
专题:
分析:作AE⊥x轴,DF⊥x轴分别于E,F,根据等腰梯形的性质,分别求出BE和DF的长,即可解答此题.
解答: 解:作AE⊥x轴,DF⊥x轴分别于E,F.
解:作AE⊥x轴,DF⊥x轴分别于E,F.
∵四边形ABCD是等腰梯形,
∴∠ABC=∠DCB,AD∥BC,
∴AE=DF=4,
在△ABE与△DCF中,
,
∴△ABE≌△DCF(AAS),
∴BE=CF,
在RT△ABE中,BE=
=
=3,
∴CF=3,
∵点C的坐标为(9,0),
∴BC=9,
∴BF=BC-CF=9-3=6,
∴D的坐标为(6,4)
故答案为:(6,4).
 解:作AE⊥x轴,DF⊥x轴分别于E,F.
解:作AE⊥x轴,DF⊥x轴分别于E,F.∵四边形ABCD是等腰梯形,
∴∠ABC=∠DCB,AD∥BC,
∴AE=DF=4,
在△ABE与△DCF中,
|
∴△ABE≌△DCF(AAS),
∴BE=CF,
在RT△ABE中,BE=
| AB-2AE2 |
| 52-42 |
∴CF=3,
∵点C的坐标为(9,0),
∴BC=9,
∴BF=BC-CF=9-3=6,
∴D的坐标为(6,4)
故答案为:(6,4).
点评:此题主要考查学生对等腰梯形的性质、坐标与图形性质的理解和掌握,此类等腰梯形的问题可以通过作高线转化为直角三角形或矩形的问题,求点的坐标的问题转化为求线段的长的问题.

练习册系列答案
相关题目
小明和小亮口袋里面都放有五张不同的北京奥运会福娃纪念卡,则两人分别在自己口袋里摸出一张福娃都是欢欢的概率是( )


A、
| ||
B、
| ||
C、
| ||
| D、1 |
二次函数y=ax2+x+1的图象必过点( )
| A、(0,a) |
| B、(-1,-a) |
| C、(-1,a) |
| D、(0,-a) |
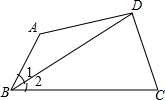 如图,BC>AB,∠1=∠2,AD=CD,探究∠BAD与∠C的关系.(用三种方法解答)
如图,BC>AB,∠1=∠2,AD=CD,探究∠BAD与∠C的关系.(用三种方法解答) 如图,点P是∠MON的平分线上的一点,A、B分别在OM、ON上,且∠APB+∠MON=180°,求证:PA=PB.
如图,点P是∠MON的平分线上的一点,A、B分别在OM、ON上,且∠APB+∠MON=180°,求证:PA=PB.