题目内容
已知,在等边△ABC中,点E在AB上,点D在CB的延长线上,且∠BED=∠ACE,求证:ED=EC.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:过点E作EF∥AC,交BC与F点,则可知△BEF为等边三角形,可证明△DBE≌△CFE,则结论可证得.
解答:
证明:过E作EF∥AC,交BC与F点,
∴∠ACE=∠CEF,
∵∠BED=∠ACF,
∴∠BED=∠FEC,
因为△ABC为等边三角形,所以△BEF为等边三角形,
∴∠DBE=∠CFE=120°,
在△DBE和△CFE中,
,
∴△DBE≌△CFE(ASA),
∴ED=EC.

证明:过E作EF∥AC,交BC与F点,
∴∠ACE=∠CEF,
∵∠BED=∠ACF,
∴∠BED=∠FEC,
因为△ABC为等边三角形,所以△BEF为等边三角形,
∴∠DBE=∠CFE=120°,
在△DBE和△CFE中,
|
∴△DBE≌△CFE(ASA),
∴ED=EC.
点评:本题主要考查三角形全等的判定和性质,解题的关键是构造三角形全等.

练习册系列答案
相关题目
小明和小亮口袋里面都放有五张不同的北京奥运会福娃纪念卡,则两人分别在自己口袋里摸出一张福娃都是欢欢的概率是( )


A、
| ||
B、
| ||
C、
| ||
| D、1 |
二次函数y=ax2+x+1的图象必过点( )
| A、(0,a) |
| B、(-1,-a) |
| C、(-1,a) |
| D、(0,-a) |
 如图所示,已知∠ABC=∠ADC=90°,AC与BD相交于点P,点E,F分别是AC,BD的中点,判断△EFP的形状.
如图所示,已知∠ABC=∠ADC=90°,AC与BD相交于点P,点E,F分别是AC,BD的中点,判断△EFP的形状.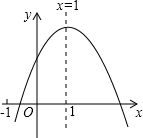 已知二次函数y=ax2+bx+c图象如图所示,下列结论:
已知二次函数y=ax2+bx+c图象如图所示,下列结论: