题目内容
已知α、β满足方程α2+3α+1=0和β2+3β+1=0，则
+
= ，
+
= ．
| β |
| α |
| α |
| β |
|
|
考点：根与系数的关系
专题：计算题
分析：根据题意得到α、β为方程x2+3x+1=0的两根，利用根与系数的关系求出α+β=-3，αβ=1，所求式子变形后将各自的值代入计算即可求出值．
解答：解：根据题意得：α、β为方程x2+3x+1=0的两根，
∴α+β=-3，αβ=1，
则
+
=
=
=
=7；
（
+
）2=
+
+2=7+2=9，即
+
=3．
故答案为：7；3．
∴α+β=-3，αβ=1，
则
| β |
| α |
| α |
| β |
| α2+β2 |
| αβ |
| (α+β)2-2αβ |
| αβ |
| 9-2 |
| 1 |
（
|
|
| β |
| α |
| α |
| β |
|
|
故答案为：7；3．
点评：此题考查了根与系数的关系，熟练掌握一元二次方程根与系数的关系是解本题的关键．
练习册系列答案
相关题目
如图，点P是∠MON的平分线上的一点，A、B分别在OM、ON上，且∠APB+∠MON=180°，求证：PA=PB．二次函数y=ax2+x+1的图象必过点（ ）
| A、（0，a） |
| B、（-1，-a） |
| C、（-1，a） |
| D、（0，-a） |
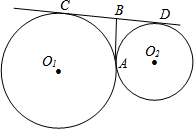半径为9cm的⊙O1和半径为4cm的⊙O2外切于点A，直线CD和和⊙O1、⊙O2分别切于C、D两点，过A的直线和⊙O1相切于A点并和直线交于B点，则CD=
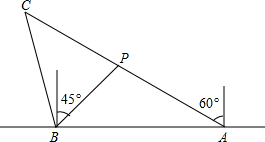如图，在一笔直的海岸线上有A，B两个观测站，A观测站在B观测站的正东方向，有一艘小船在点P处，从A处测得小船在北偏西60°方向，从B处测得小船在北偏东45°的方向，点P到点B的距离是3