题目内容
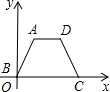 如图所示,梯形ABCD中,AB=DC=5,点A到x轴的距离是4,点C的坐标是(9,0),则梯形ABCD的面积是
如图所示,梯形ABCD中,AB=DC=5,点A到x轴的距离是4,点C的坐标是(9,0),则梯形ABCD的面积是考点:坐标与图形性质,三角形的面积
专题:计算题
分析:作AE⊥OC于E,DF⊥OC于F,如图,在Rt△AOE中,根据勾股定理计算出OE=3,由于梯形ABCD为等腰梯形,则CF=OE=3,于是可得到EF=3,则AD=EF=3,然后根据梯形的面积公式计算.
解答:解: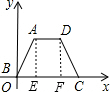 作AE⊥OC于E,DF⊥OC于F,如图,
作AE⊥OC于E,DF⊥OC于F,如图,
在Rt△AOE中,∵AB=5,AE=4,
∴OE=
=3,
∵梯形ABCD中,AB=DC=5,
∴梯形ABCD为等腰梯形,
∴CF=OE=3,
而OC=9,
∴EF=9-3-3=3,
∴AD=EF=3,
∴梯形ABCD的面积=
×(3+9)×4=24.
故答案为24.
 作AE⊥OC于E,DF⊥OC于F,如图,
作AE⊥OC于E,DF⊥OC于F,如图,在Rt△AOE中,∵AB=5,AE=4,
∴OE=
| AB2-AE2 |
∵梯形ABCD中,AB=DC=5,
∴梯形ABCD为等腰梯形,
∴CF=OE=3,
而OC=9,
∴EF=9-3-3=3,
∴AD=EF=3,
∴梯形ABCD的面积=
| 1 |
| 2 |
故答案为24.
点评:本题考查了坐标与图形:利用点的坐标求相应线段的长和判断线段与坐标轴的位置关系;已知图形中一些点的坐标求面积时,过已知点向坐标轴作垂线,然后求出相关的线段长,是解决这类问题的基本方法和规律.

练习册系列答案
相关题目
 如图,已知在△ABC中,DE∥BC,AE是AF、AC的比例中项,求证:DF∥BE.
如图,已知在△ABC中,DE∥BC,AE是AF、AC的比例中项,求证:DF∥BE.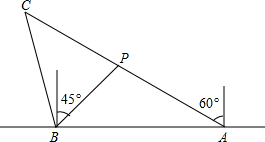 如图,在一笔直的海岸线上有A,B两个观测站,A观测站在B观测站的正东方向,有一艘小船在点P处,从A处测得小船在北偏西60°方向,从B处测得小船在北偏东45°的方向,点P到点B的距离是3
如图,在一笔直的海岸线上有A,B两个观测站,A观测站在B观测站的正东方向,有一艘小船在点P处,从A处测得小船在北偏西60°方向,从B处测得小船在北偏东45°的方向,点P到点B的距离是3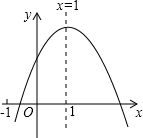 已知二次函数y=ax2+bx+c图象如图所示,下列结论:
已知二次函数y=ax2+bx+c图象如图所示,下列结论: