题目内容
计算下列各式:
(1)3
+
-4
(2)(
+
)2-(
-
)2
(3)(2-
)2005(2+
)2006
(4)(
+
+
)(
-
-
)
(1)3
| 18 |
| 1 |
| 5 |
| 50 |
|
(2)(
| 5 |
| 2 |
| 5 |
| 2 |
(3)(2-
| 5 |
| 5 |
(4)(
| 3 |
| 2 |
| 5 |
| 3 |
| 2 |
| 5 |
考点:二次根式的混合运算
专题:计算题
分析:(1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先利用平方差公式得到原式=(
+
+
-
)(
+
-
+
),然后合并后进行二次根式的乘法运算;
(3)先根据积的乘方得到原式=[(2-
)(2+
)]2005•(2+
),然后利用平方差公式计算;
(4)先变形得到原式=[
+(
+
)]•[
-(
+
)],然后利用平方差公式和完全平方公式计算.
(2)先利用平方差公式得到原式=(
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
(3)先根据积的乘方得到原式=[(2-
| 5 |
| 5 |
| 5 |
(4)先变形得到原式=[
| 3 |
| 2 |
| 5 |
| 3 |
| 2 |
| 5 |
解答:解:(1)原式=9
+
-2
=8
;
(2)原式=(
+
+
-
)(
+
-
+
)
=2
•2
=4
;
(3)原式=[(2-
)(2+
)]2005•(2+
)
=(4-5)2005•(2+
)
=-(2+
)
=-2-
;
(4)原式=[
+(
+
)]•[
-(
+
)]
=(
)2-(
+
)2
=3-(2+2
+5)
=3-7-2
=-4-2
.
| 2 |
| 2 |
| 2 |
=8
| 2 |
(2)原式=(
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
=2
| 5 |
| 2 |
=4
| 10 |
(3)原式=[(2-
| 5 |
| 5 |
| 5 |
=(4-5)2005•(2+
| 5 |
=-(2+
| 5 |
=-2-
| 5 |
(4)原式=[
| 3 |
| 2 |
| 5 |
| 3 |
| 2 |
| 5 |
=(
| 3 |
| 2 |
| 5 |
=3-(2+2
| 10 |
=3-7-2
| 10 |
=-4-2
| 10 |
点评:本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
二次函数y=ax2+x+1的图象必过点( )
| A、(0,a) |
| B、(-1,-a) |
| C、(-1,a) |
| D、(0,-a) |
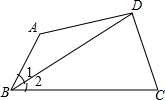 如图,BC>AB,∠1=∠2,AD=CD,探究∠BAD与∠C的关系.(用三种方法解答)
如图,BC>AB,∠1=∠2,AD=CD,探究∠BAD与∠C的关系.(用三种方法解答) 如图所示,已知∠ABC=∠ADC=90°,AC与BD相交于点P,点E,F分别是AC,BD的中点,判断△EFP的形状.
如图所示,已知∠ABC=∠ADC=90°,AC与BD相交于点P,点E,F分别是AC,BD的中点,判断△EFP的形状.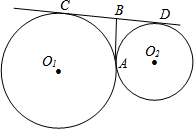 半径为9cm的⊙O1和半径为4cm的⊙O2外切于点A,直线CD和和⊙O1、⊙O2分别切于C、D两点,过A的直线和⊙O1相切于A点并和直线交于B点,则CD=
半径为9cm的⊙O1和半径为4cm的⊙O2外切于点A,直线CD和和⊙O1、⊙O2分别切于C、D两点,过A的直线和⊙O1相切于A点并和直线交于B点,则CD=